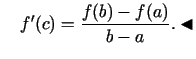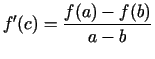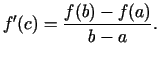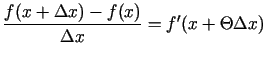Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.4. Košī teorēma (Teorēma par funkciju
Augstāk: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
Iepriekšējais: 2.2. Rolla teorēma (Teorēma par atvasinājuma
2.3. teorēma. Ja funkcija  nepārtraukta slēgtā
intervālā
nepārtraukta slēgtā
intervālā ![$ [a;b]$](img437.gif) un ir diferencējama šī intervāla iekšējos
punktos, tad eksistē vismaz viens tāds intervāla iekšējais punkts
un ir diferencējama šī intervāla iekšējos
punktos, tad eksistē vismaz viens tāds intervāla iekšējais punkts
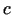 , kurā
, kurā
 Izveidosim palīgfunkciju
Izveidosim palīgfunkciju
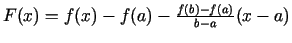 . Šī funkcija
. Šī funkcija 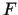 apmierina visus Rolla teorēmas nosacījumus: nepārtraukta intervālā
apmierina visus Rolla teorēmas nosacījumus: nepārtraukta intervālā
![$ [a;b]$](img437.gif) , diferencējama tā iekšējos punktos (jo šādas īpašības
piemīt funkcijai
, diferencējama tā iekšējos punktos (jo šādas īpašības
piemīt funkcijai  ) un
) un 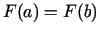 , jo
, jo 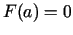 un
un 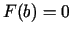 .
Saskaņā ar Rolla teorēmu eksistē tāds
.
Saskaņā ar Rolla teorēmu eksistē tāds
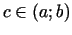 , ka
, ka 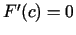 .
.
Tā kā
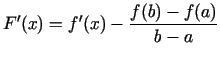
un
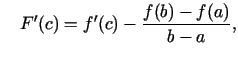
tad
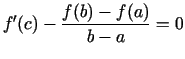
jeb
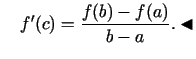
Lai sniegtu Lagranža teorēmai ģeometrisko interpretāciju,
izveidosim šādu zīmējumu (2.4. zīm.).
No taisnleņķa trijstūra 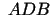 :
:
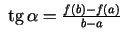 . Šī attiecība no ģ
eometriskā viedokļa izsaka hordas
. Šī attiecība no ģ
eometriskā viedokļa izsaka hordas 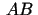 virziena
koeficientu. Tā kā
virziena
koeficientu. Tā kā
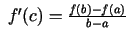 un
un 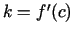 ir
funkcijas grafikam punktā
ir
funkcijas grafikam punktā 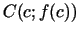 novilktās pieskares virziena
koeficients, tad var teikt, ka saskaņā ar Lagranža teorēmu uz
grafika eksistē tāds punkts, kurā novilktā pieskare ir paralēla
hordai
novilktās pieskares virziena
koeficients, tad var teikt, ka saskaņā ar Lagranža teorēmu uz
grafika eksistē tāds punkts, kurā novilktā pieskare ir paralēla
hordai 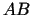 .
.
-
2.3. piezīme.
- Arī šoreiz tādi punkti
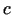 var būt
vairāki un visi Lagranža teorēmas nosacījumi ir būtiski.
var būt
vairāki un visi Lagranža teorēmas nosacījumi ir būtiski.
Pieņemsim, ka visi Lagranža teorēmas nosacījumi izpildās intervālā
![$ [b;a]$](img472.gif) (šoreiz
(šoreiz 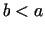 ).
).
Saskaņā ar teorēmu eksistē tāds
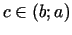 , kurā
, kurā
jeb
Tātad Lagranža teorēmas formula ir spēkā gan 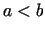 , gan
, gan 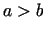 .
Starpvērtību
.
Starpvērtību 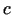 ir izdevīgi pierakstīt formā
ir izdevīgi pierakstīt formā
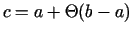 ,
kur
,
kur
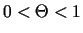 . Ja šajā formulā ievieto
. Ja šajā formulā ievieto 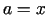 ,
,
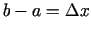 un
un
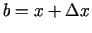 , tad iegūst formulu
, tad iegūst formulu
jeb
Šo formulu sauc par Lagranža galīgo pieaugumu formulu
(turpmāk: Lagranža formulu).



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.4. Košī teorēma (Teorēma par funkciju
Augstāk: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
Iepriekšējais: 2.2. Rolla teorēma (Teorēma par atvasinājuma
2002-01-21
![]() nepārtraukta slēgtā
intervālā
nepārtraukta slēgtā
intervālā ![]() un ir diferencējama šī intervāla iekšējos
punktos, tad eksistē vismaz viens tāds intervāla iekšējais punkts
un ir diferencējama šī intervāla iekšējos
punktos, tad eksistē vismaz viens tāds intervāla iekšējais punkts
![]() , kurā
, kurā
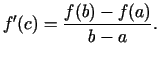
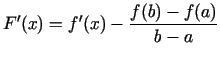 un
un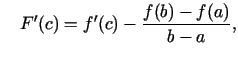
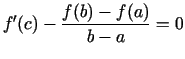 jeb
jeb