


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.3. Lagranža teorēma
Augstāk: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
Iepriekšējais: 2.1. Fermā teorēma
2.2. teorēma. [Rolla2.1 teorēma] Ja funkcija  nepārtraukta slēgtā
intervālā
nepārtraukta slēgtā
intervālā ![$ [a;b]$](img437.gif) , diferencējama šī intervāla iekšējos
punktos un šī intervāla galapunktos funkcijas vērtības ir
vienādas, t.i.,
, diferencējama šī intervāla iekšējos
punktos un šī intervāla galapunktos funkcijas vērtības ir
vienādas, t.i., 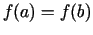 , tad eksistē vismaz viens tāds
intervāla iekšējais punkts
, tad eksistē vismaz viens tāds
intervāla iekšējais punkts 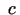 , kurā
, kurā 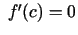 .
.
 Apzīmēsim ar
Apzīmēsim ar 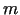 un
un 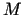 attiecīgi funkcijas
vismazāko un vislielāko vērtību intervālā
attiecīgi funkcijas
vismazāko un vislielāko vērtību intervālā ![$ [a;b]$](img437.gif) . (Šādas vērtības
eksistē, jo funkcija ir nepārtraukta šajā intervālā).
. (Šādas vērtības
eksistē, jo funkcija ir nepārtraukta šajā intervālā).
Ja 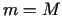 , tad intervālā
, tad intervālā ![$ [a;b]$](img437.gif)
 ir konstanta funkcija un
jebkurā tā punktā
ir konstanta funkcija un
jebkurā tā punktā 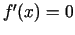 .
.
Ja 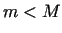 , tad vismaz viens no šiem skaitļiem
, tad vismaz viens no šiem skaitļiem 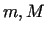 atšķiras no
skaitļa
atšķiras no
skaitļa 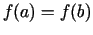 , piemēram,
, piemēram,
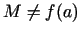 . Seko, ka funkcija
. Seko, ka funkcija  savu vislielāko vērtību
savu vislielāko vērtību 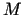 sasniedz šī intervāla kādā iekšējā
punktā
sasniedz šī intervāla kādā iekšējā
punktā 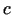 , t.i., eksistē tāds
, t.i., eksistē tāds
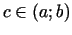 , ka
, ka 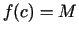 . Saskaņā
ar Fermā teorēmu
. Saskaņā
ar Fermā teorēmu 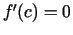 .
.
-
2.2. piezīme.
-

- Rolla teorēmai ir šāda ģeometriska
interpretācija: uz funkcijas grafika eksistē tāds punkts
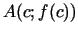 , kurā novilktā pieskare ir horizontāla
(2.2. zīm.).
, kurā novilktā pieskare ir horizontāla
(2.2. zīm.).
- Tādi punkti, kuros atvasinājums ir nulle, var būt
vairāki (2.3. zīm.).
- Ja
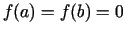 , tad Rolla teorēma apgalvo, ka starp
divām funkcijas nullēm2.2 eksistē vismaz viena atvasinājuma nulle.
, tad Rolla teorēma apgalvo, ka starp
divām funkcijas nullēm2.2 eksistē vismaz viena atvasinājuma nulle.
- Visi teorēmas nosacījumi ir būtiski, piemēram,
funkcijai
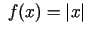 intervālā
intervālā ![$ [-1,1]$](img451.gif) teorēma nav spēkā, jo
punktā
teorēma nav spēkā, jo
punktā 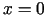 šī funkcija nav diferencējama.
šī funkcija nav diferencējama.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.3. Lagranža teorēma
Augstāk: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
Iepriekšējais: 2.1. Fermā teorēma
2002-01-21
![]() nepārtraukta slēgtā
intervālā
nepārtraukta slēgtā
intervālā ![]() , diferencējama šī intervāla iekšējos
punktos un šī intervāla galapunktos funkcijas vērtības ir
vienādas, t.i.,
, diferencējama šī intervāla iekšējos
punktos un šī intervāla galapunktos funkcijas vērtības ir
vienādas, t.i., ![]() , tad eksistē vismaz viens tāds
intervāla iekšējais punkts
, tad eksistē vismaz viens tāds
intervāla iekšējais punkts ![]() , kurā
, kurā ![]() .
.