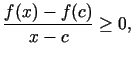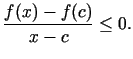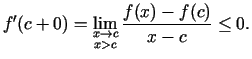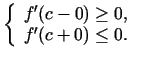Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.2. Rolla teorēma (Teorēma par atvasinājuma
Augstāk: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
Iepriekšējais: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
2.1. teorēma. Ja intervālā
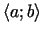 definētā funkcija šī intervāla iekšējā punktā
definētā funkcija šī intervāla iekšējā punktā 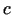 sasniedz savu
vismazāko vai vislielāko vērtību un ir diferencējama
šajā punktā, tad
sasniedz savu
vismazāko vai vislielāko vērtību un ir diferencējama
šajā punktā, tad 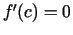 .
.
 Pieņemsim, ka punktā
Pieņemsim, ka punktā 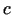 funkcija
funkcija  sasniedz savu vislielāko vērtību, t.i., visiem
sasniedz savu vislielāko vērtību, t.i., visiem
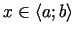 izpildās
izpildās
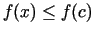 . Sastādīsim attiecību
. Sastādīsim attiecību
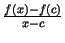 un novērtēsim tās zīmi.
un novērtēsim tās zīmi.
Ja 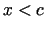 , tad
, tad
ja 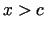 , tad
, tad
(Skaitītājs abos gadījumos ir nepozitīvs, t.i.,
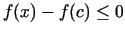 ).
).
Atradīsim šai attiecībai vienpusējās robežas punktā 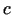 . Robeža no
kreisās puses būs vienāda ar funkcijas atvasinājumu no
kreisās puses punktā
. Robeža no
kreisās puses būs vienāda ar funkcijas atvasinājumu no
kreisās puses punktā 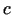 , pie tam
, pie tam
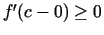 .
.
Analogi
(Vienpusējie atvasinājumi eksistē un tie ir vienādi ar 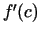 , jo
funkcija ir diferencējama šajā punktā).
, jo
funkcija ir diferencējama šajā punktā).
Esam ieguvuši, ka
Tādējādi 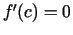 .
.
-
2.1. piezīme.
-

- Analogi apskata otru gadījumu, kad funkcija punktā
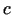 sasniedz savu vismazāko vērtību.
sasniedz savu vismazāko vērtību.
- Funkcijas grafikam atbilstošajā punktā
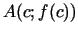 novilktā pieskare ir horizontāla (2.1. zīm.).
novilktā pieskare ir horizontāla (2.1. zīm.).



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.2. Rolla teorēma (Teorēma par atvasinājuma
Augstāk: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
Iepriekšējais: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
2002-01-21
![]() definētā funkcija šī intervāla iekšējā punktā
definētā funkcija šī intervāla iekšējā punktā ![]() sasniedz savu
vismazāko vai vislielāko vērtību un ir diferencējama
šajā punktā, tad
sasniedz savu
vismazāko vai vislielāko vērtību un ir diferencējama
šajā punktā, tad ![]() .
.