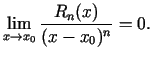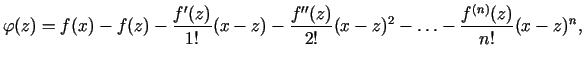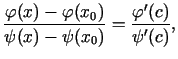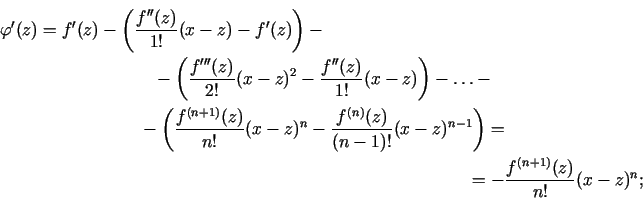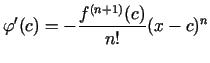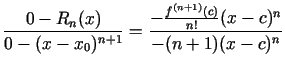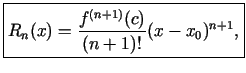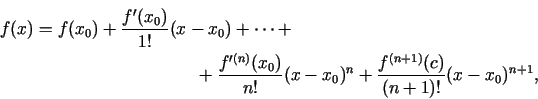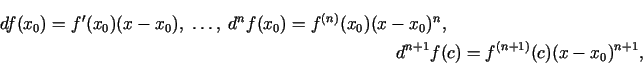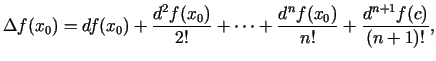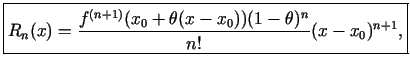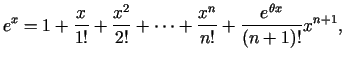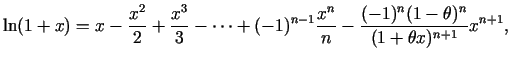Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.7. Jautājumi
Augstāk: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
Iepriekšējais: 2.5. Lopitāla kārtula
Teilora 2.5 formulā funkcija tiek aproksimēta (tuvināti
izteikta) ar polinomiem, kurus sauc par Teilora polinomiem.
Teilora formulu lieto gan diferencējamas funkcijas vērtību
tuvinātai aprēķināšanai, gan teorētisku jautājumu apskatā.
Pieņemsim, ka funkcija  ir
ir 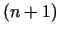 reizi diferencējama punkta
reizi diferencējama punkta
 apkārtnē. Noteiksim tādu
apkārtnē. Noteiksim tādu 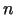 -tās pakāpes polinomu
-tās pakāpes polinomu 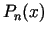 ,
lai tas aproksimētu doto funkciju
,
lai tas aproksimētu doto funkciju  punkta
punkta  apkārtnē. Par šo aproksimācijas polinomu izraudzīsimies šādu
polinomu
apkārtnē. Par šo aproksimācijas polinomu izraudzīsimies šādu
polinomu
(Acīmredzot,
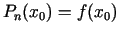 ,
,
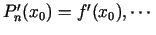 ,
,
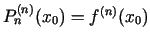 ).
).
2.1. definīcija. Polinomu 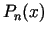 , kas ir definēts ar formulu
(2.1), sauc par funkcijas
, kas ir definēts ar formulu
(2.1), sauc par funkcijas 
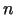 -tās pakāpes Teilora
polinomu pēc
-tās pakāpes Teilora
polinomu pēc 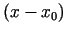 pakāpēm. Polinoma koeficientus
pakāpēm. Polinoma koeficientus
sauc par Teilora koeficientiem.
Starpību
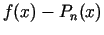 apzīmēsim ar
apzīmēsim ar 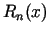 , kas ir
aptuvenās vienādības
, kas ir
aptuvenās vienādības
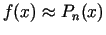 kļūda.
kļūda.
Tātad
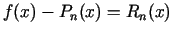 jeb
jeb
2.2. definīcija. Vienādību (2.2) sauc par funkcijas  Teilora
formulu punkta
Teilora
formulu punkta  apkārtnē (jeb pēc
apkārtnē (jeb pēc 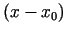 pakāpēm), bet
pakāpēm), bet
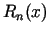 - par tās atlikuma locekli.
- par tās atlikuma locekli.
Izmantojot 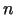 reizes Lopitāla kārtulu, var parādīt, ka atlikuma
loceklis
reizes Lopitāla kārtulu, var parādīt, ka atlikuma
loceklis
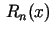 ir augstākas kārtas bezgalīgi maza
funkcija salīdzinājumā ar
ir augstākas kārtas bezgalīgi maza
funkcija salīdzinājumā ar
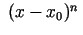 , kad
, kad
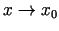 , t.i.,
, t.i.,
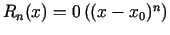 , kad
, kad
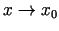 .
.
Bez šīs formas atlikuma loceklim var būt arī citas formas.
Aplūkosim, kā tas izskatās Lagranža formā vai Košī formā.
Izveidosim šādu funkciju
kur 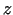 atrodas starp
atrodas starp  un
un  (
( - fiksēts punkts no
- fiksēts punkts no  apkārtnes).
apkārtnes).
Kā otru funkciju izvēlēsimies
Abas šīs funkcijas slēgtajā intervālā, kura galapunkti ir  un
un
 , apmierina Košī teorēmas nosacījumus, tāpēc
, apmierina Košī teorēmas nosacījumus, tāpēc
kur
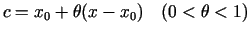 .
.
Ņemot vērā formulas, kas uzdod šīs funkcijas, iegūsim, ka
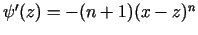 .
.
Tātad
un
Košī teorēmas formula iegūs šādu izskatu
jeb
kur
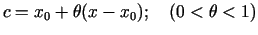 .
.
Šādi izsakās Teilora formulas atlikuma loceklis Lagranža
formā. Parasti precīza 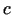 vērtība nav zināma: var apgalvot tikai
to, ka
vērtība nav zināma: var apgalvot tikai
to, ka 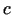 atrodas starp
atrodas starp  un
un  .
.
Teilora formula ar atlikuma locekli Lagranža formā izskatās šādi:
kur
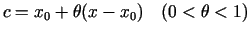 .
.
Apzīmējot
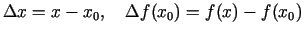 ,
,
šī formula pārrakstās šādi:
kur
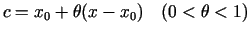 .
.
-
2.7. piezīme.
- Ievietojot
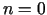 , iegūsim Teilora formulas atsevišķu gadījumu, kas ir Lagranža formula.
, iegūsim Teilora formulas atsevišķu gadījumu, kas ir Lagranža formula.
Tagad funkciju 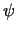 izvēlēsimies šādu:
izvēlēsimies šādu:
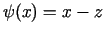 . Arī šoreiz
funkcijām
. Arī šoreiz
funkcijām 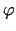 un
un 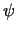 pielietosim Košī teorēmu. Iegūsim
Teilora formulas atlikuma locekli Košī formā:
pielietosim Košī teorēmu. Iegūsim
Teilora formulas atlikuma locekli Košī formā:
kur
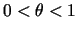 .
.
-
2.7. piemērs.
- Funkcijai
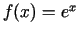 uzrakstīt Teilora formulu ar
atlikuma locekli Lagranža formā.
uzrakstīt Teilora formulu ar
atlikuma locekli Lagranža formā.
Uzrakstīsim Teilora formulu pēc  pakāpēm (jeb punkta
pakāpēm (jeb punkta 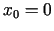 apkārtnē). Šai funkcijai
apkārtnē). Šai funkcijai
Tātad
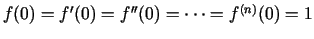 un
un
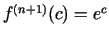 , kur
, kur
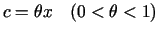 .
.
Teilora formula ar atlikuma locekli Lagranža formā šai funkcijai
izskatās:
kur
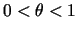 .
.
-
2.8. piemērs.
- Funkcijai
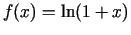 uzrakstīt Teilora formulu
ar atlikuma locekli Košī formā.
uzrakstīt Teilora formulu
ar atlikuma locekli Košī formā.
Šai funkcijai uzrakstīsim Teilora formulu punkta 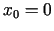 apkārtnē.
Šoreiz
apkārtnē.
Šoreiz
Tātad
kur
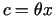 ,
,
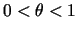 .
.
Teilora formula ar atlikuma locekli Košī formā šai funkcijai
izskatās:
kur
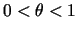 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.7. Jautājumi
Augstāk: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
Iepriekšējais: 2.5. Lopitāla kārtula
2002-01-21
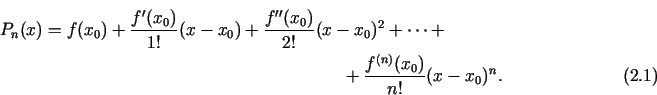
![]() , kas ir definēts ar formulu
(2.1), sauc par funkcijas
, kas ir definēts ar formulu
(2.1), sauc par funkcijas ![]()
![]() -tās pakāpes Teilora
polinomu pēc
-tās pakāpes Teilora
polinomu pēc ![]() pakāpēm. Polinoma koeficientus
pakāpēm. Polinoma koeficientus
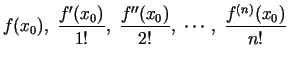
![]() Teilora
formulu punkta
Teilora
formulu punkta ![]() apkārtnē (jeb pēc
apkārtnē (jeb pēc ![]() pakāpēm), bet
pakāpēm), bet
![]() - par tās atlikuma locekli.
- par tās atlikuma locekli.