Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.10. Jautājumi
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3.8. Funkcijas grafika asimptotas
Izpētīt funkciju nozīmē noskaidrot, kā mainās tās raksturs,
mainoties argumentam. Ņemot vērā funkcijas pētīšanā iegūtos
rezultātus, konstruē tās grafiku.
Funkciju ar atvasinājuma palīdzību parasti pēta pēc šādas shēmas.
- Atrod funkcijas definīcijas apgabalu
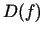 , nosaka
pārtraukuma punktus un to veidu, norāda funkcijas nepārtrauktības
intervālus.
, nosaka
pārtraukuma punktus un to veidu, norāda funkcijas nepārtrauktības
intervālus.
- Noskaidro, vai
 ir pāra funkcija, nepāra funkcija,
periodiska funkcija.
ir pāra funkcija, nepāra funkcija,
periodiska funkcija.
- Atrod funkcijas grafika krustpunktus ar koordinātu
asīm un nosaka intervālus, kuros tā ir negatīva, un intervālus,
kuros funkcija ir pozitīva.
- Nosaka funkcijas monotonitātes intervālus un
ekstrēmus.
- Nosaka funkcijas grafika izliekuma un ieliekuma intervālus,
kā arī grafika pārliekuma punktus.
- Atrod funkcijas grafika asimptotas.
-
3.13. piezīme.
-

- Funkcijas grafika precizēšanai vajadzības
gadījumā vēl var atrast funkcijas vērtības izraudzītajos
papildpunktos.
- Pāra vai nepāra funkciju vienkāršības
labad var pētīt tikai pozitīvajām argumenta vērtībām.
Izmantojot pāra (vai nepāra) funkciju īpašības, izdara secinājumus
par tās raksturu visā tās definīcijas apgabalā. Savukārt
periodiskas funkcijas var pētīt tikai intervālā, kura garums ir
vienāds ar tās periodu.
- Pirms uzzīmē funkcijas grafiku, koordinātu
plaknē atzīmē visus funkcijai raksturīgos3.9 punktus un grafika asimptotas.
-
3.17. piemērs.
- Izpētīt funkciju
![$ f(x)=\sqrt[3]{x^2}\cdot e^x$](img861.gif) un uzzīmēt tās grafiku.
un uzzīmēt tās grafiku.
-
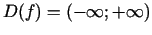 . Funkcijai pārtraukuma punktu nav,
. Funkcijai pārtraukuma punktu nav,
 - nepārtraukta funkcija.
- nepārtraukta funkcija.
- Funkcija nav ne pāra, ne nepāra, tā ir neperiodiska.
- Argumenta vērtībai
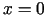 atbilst funkcijas
vērtība
atbilst funkcijas
vērtība 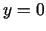 . Funkcija ir nenegatīva visā savā definīcijas
apgabalā.
. Funkcija ir nenegatīva visā savā definīcijas
apgabalā.
- Atradīsim
Funkcijas kritiskie punkti ir
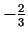 un 0.
un 0.
Atvasinājuma zīmes atzīmēsim uz skaitļu taisnes
(3.25. zīm.).
Funkcija aug intervālos
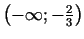 un
un
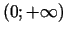 , dilst intervālā
, dilst intervālā
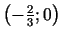 .
.
- Atradīsim
Otrās kārtas atvasinājums ir nulle punktos
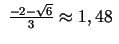 un
un
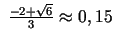 ; bezgalīgs punktā
; bezgalīgs punktā 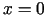 .
.
Otrās kārtas atvasinājuma zīmes atzīmēsim uz skaitļu taisnes
(3.26. zīm.).
Funkcijas grafiks ir ieliekts intervālos
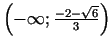 un
un
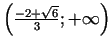 , izliekts intervālā
, izliekts intervālā
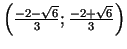 .
.
Funkcijas grafika punkti, kuru abscisas ir
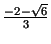 un
un
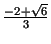 , ir grafika pārliekuma punkti.
, ir grafika pārliekuma punkti.
- Vertikālo asimptotu grafikam nav.
Atradīsim
Tādējādi grafikam slīpās asimptotas, kad
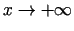 ,
nav.
,
nav.
Tādējādi taisne 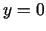 ir grafika horizontālā asimptota, kad
ir grafika horizontālā asimptota, kad
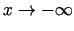 .
.
Funkcijas pētīšanā iegūtos rezultātus ir lietderīgi apkopot
šādā tabulā:
Funkcijas grafiks attēlots 3.27. zīmējumā.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.10. Jautājumi
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3.8. Funkcijas grafika asimptotas
2002-01-21
![$\displaystyle f'(x)=\frac{2}{3}x^{-\frac{1}{3}}e^x+\sqrt[3]{x^2}e^x=\frac{(2+3x)e^x}{3\sqrt[3]{x}}\/.$](img864.gif)
![$\displaystyle \max f(x)=f\left(-\frac{2}{3}\right)=\sqrt[3]{\frac{4}{9}}\cdot e^{-\frac{2}{3}}
\approx 0,39\/;\quad \min f(x)=f(0)=0\/.$](img869.gif)
![$\displaystyle f''(x)=\frac{9x^2+12x-2}{9x\sqrt[3]{x}}e^x\/.$](img870.gif)
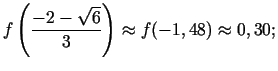
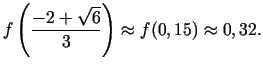
![$\displaystyle k_1=\lim\limits_{x\rightarrow
+\infty}\frac{f(x)}{x}=\lim\limits_{x\rightarrow
+\infty}\frac{e^x}{\sqrt[3]{x}}=+\infty\/.$](img881.gif)
![$\displaystyle =\lim\limits_{x\rightarrow -\infty}\frac{f(x)}{x}=\lim\limits_{x\rightarrow +-\infty}\frac{e^x}{\sqrt[3]{x}}=0\/;$](img883.gif)