Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.9. Funkcijas pilnā pētīšana
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3.7. Funkcijas grafika pārliekuma punkti un
3.9. definīcija. Taisni 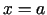 sauc par funkcijas
sauc par funkcijas  grafika vertikālo
asimptotu, ja vismaz viena no vienpusējām robežām
grafika vertikālo
asimptotu, ja vismaz viena no vienpusējām robežām
Piemēram, funkcijas
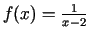 grafikam taisne
grafikam taisne 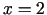 ir
vertikālā asimptota, jo
ir
vertikālā asimptota, jo
-
3.11. piezīme.
- Ja punkts
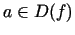 un taisne
un taisne 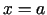 ir funkcijas
ir funkcijas  grafika vertikālā asimptota, tad acīmredzami
grafika vertikālā asimptota, tad acīmredzami 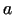 ir šīs funkcijas
otrā veida pārtraukuma punkts.
ir šīs funkcijas
otrā veida pārtraukuma punkts.
3.10. definīcija. Taisni 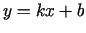 sauc par funkcijas
sauc par funkcijas  grafika
slīpo asimptotu, kad
grafika
slīpo asimptotu, kad
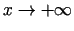 , ja funkciju var
uzrakstīt šādā izskatā:
, ja funkciju var
uzrakstīt šādā izskatā:
kur
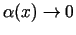 , kad
, kad
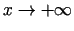 .
.
Piemēram, taisne 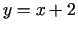 ir funkcijas
ir funkcijas
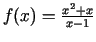 grafika slīpā asimptota, kad
grafika slīpā asimptota, kad
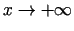 , jo
, jo
un
3.9. teorēma. (Funkcijas grafika slīpās asimptotas eksistences
nepieciešamais un pietiekamais nosacījums)
Lai taisne 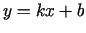 būtu funkcijas
būtu funkcijas  grafika slīpā asimptota,
kad
grafika slīpā asimptota,
kad
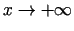 , ir nepieciešami un pietiekami, lai
eksistētu galīgas robežas
, ir nepieciešami un pietiekami, lai
eksistētu galīgas robežas
 Nepieciešamība. Tā kā taisne
Nepieciešamība. Tā kā taisne 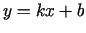 ir funkcijas grafika slīpā asimptota, kad
ir funkcijas grafika slīpā asimptota, kad
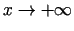 ,
tad šo funkciju var uzrakstīt izskatā:
,
tad šo funkciju var uzrakstīt izskatā:
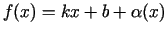 , kur
, kur
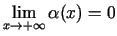 .
.
Savukārt no šīs vienādības izriet šādas divas vienādības:
Šo divu vienādību labajām pusēm eksistē galīgas robežas, kad
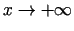 , kas atbilstoši ir
, kas atbilstoši ir 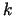 un
un 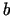 . Tāpēc
eksistē galīgas robežas arī kreisajām pusēm un tās ir vienādas
atbilstoši ar
. Tāpēc
eksistē galīgas robežas arī kreisajām pusēm un tās ir vienādas
atbilstoši ar 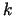 un
un 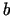 , t.i.,
, t.i.,
Pietiekamība. Tā kā eksistē galīgas robežas
tad saskaņā ar robežas īpašībām funkcija 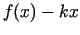 atšķiras no
savas robežas
atšķiras no
savas robežas 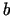 par bezgalīgi mazu funkciju
par bezgalīgi mazu funkciju 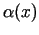 , kad
, kad
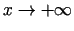 .
.
Tātad
jeb
kur
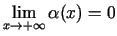 .
.
Tādējādi taisne 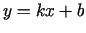 ir funkcijas
ir funkcijas  grafika slīpā asimptota,
kad
grafika slīpā asimptota,
kad
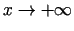 .
.
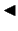
Analogi definē funkcijas  grafika slīpo asimptotu, kad
grafika slīpo asimptotu, kad
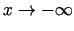 , analogi formulē un pierāda funkcijas
grafika slīpās asimptotas, kad
, analogi formulē un pierāda funkcijas
grafika slīpās asimptotas, kad
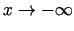 , eksistences
nepieciešamo un pietiekamo nosacījumu.
, eksistences
nepieciešamo un pietiekamo nosacījumu.
-
3.12. piezīme.
-

- Atsevišķām funkcijām taisne
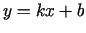 ir
grafika slīpā asimptota gan, kad
ir
grafika slīpā asimptota gan, kad
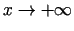 , gan, kad
, gan, kad
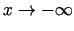 .
.
- Ja
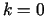 , tad iegūstam funkcijas grafika horizontālo asimptotu, kad
, tad iegūstam funkcijas grafika horizontālo asimptotu, kad
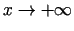 , vai
, vai
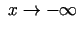 .
.
- Ja vismaz viena no 3.9. teorēmā
minētajām robežām neeksistē vai ir bezgalīga, tad funkcijas
grafikam slīpās asimptotas, kad
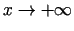 ,
nav.
,
nav.
-
3.13. piemērs.
- Atrast funkcijas
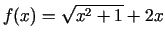 grafika
asimptotas.
grafika
asimptotas.
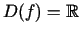 , vertikālo asimptotu funkcijas grafikam nav.
Vispirms atradīsim grafika slīpo asimptotu, kad
, vertikālo asimptotu funkcijas grafikam nav.
Vispirms atradīsim grafika slīpo asimptotu, kad
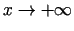 .
.
Tādējādi taisne 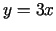 ir funkcijas grafika slīpā asimptota, kad
ir funkcijas grafika slīpā asimptota, kad
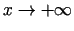 .
.
Analogi atradīsim grafika slīpo asimptotu, kad
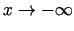 .
.
Šoreiz
Tādējādi taisne 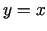 ir funkcijas grafika slīpā asimptota, kad
ir funkcijas grafika slīpā asimptota, kad
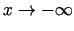 .
.
Funkcijas
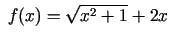 grafiks un tā slīpās
asimptotas, kad
grafiks un tā slīpās
asimptotas, kad
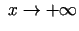 un kad
un kad
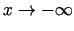 , ir attēloti 3.21. zīmējumā.
, ir attēloti 3.21. zīmējumā.
-
3.14. piemērs.
- Atrast funkcijas
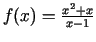 grafika
asimptotas.
grafika
asimptotas.
Funkcija nav definēta punktā 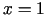 . Taisne
. Taisne 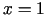 ir šīs funkcijas
grafika vertikālā asimptota, jo
ir šīs funkcijas
grafika vertikālā asimptota, jo
Šoreiz
Tādējādi taisne 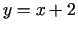 ir funkcijas grafika slīpā asimptota, kad
ir funkcijas grafika slīpā asimptota, kad
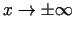 (3.22. zīm.).
(3.22. zīm.).
-
3.15. piemērs.
- Atrast funkcijas
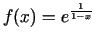 grafika
asimptotas.
grafika
asimptotas.
Funkcija nav definēta punktā 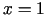 . Taisne
. Taisne 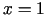 ir šīs funkcijas
grafika vertikālā asimptota, jo
ir šīs funkcijas
grafika vertikālā asimptota, jo
Starp citu,
Šoreiz
Tādējādi taisne 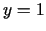 ir šīs funkcijas grafika horizontālā
asimptota, kad
ir šīs funkcijas grafika horizontālā
asimptota, kad
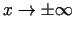 (3.23. zīm.).
(3.23. zīm.).
-
3.16. piemērs.
- Atrast funkcijas
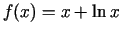 grafika asimptotas.
grafika asimptotas.
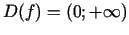 . Taisne
. Taisne 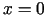 ir funkcijas grafika vertikālā
asimptota, jo
ir funkcijas grafika vertikālā
asimptota, jo
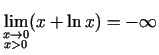 .
.
Tādējādi grafikam slīpā asimptota, kad
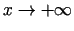 ,
neeksistē (3.24. zīm.).
,
neeksistē (3.24. zīm.).



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.9. Funkcijas pilnā pētīšana
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3.7. Funkcijas grafika pārliekuma punkti un
2002-01-21
![]() sauc par funkcijas
sauc par funkcijas ![]() grafika vertikālo
asimptotu, ja vismaz viena no vienpusējām robežām
grafika vertikālo
asimptotu, ja vismaz viena no vienpusējām robežām
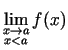 vai
vai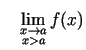 ir
ir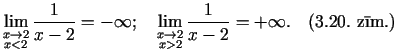
![]() sauc par funkcijas
sauc par funkcijas ![]() grafika
slīpo asimptotu, kad
grafika
slīpo asimptotu, kad
![]() , ja funkciju var
uzrakstīt šādā izskatā:
, ja funkciju var
uzrakstīt šādā izskatā:
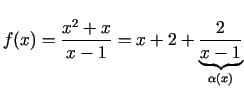
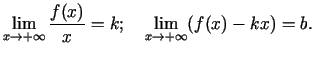
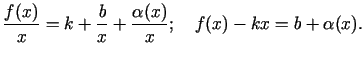
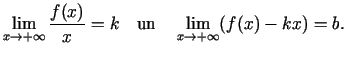
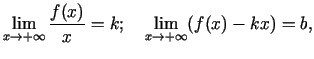
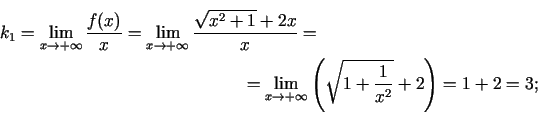
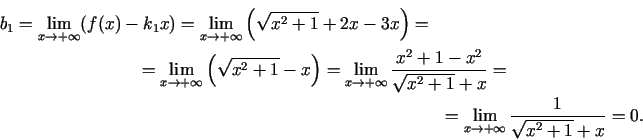
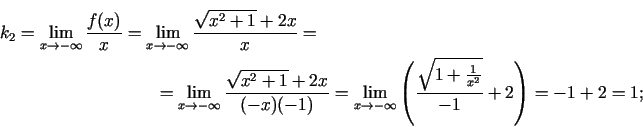
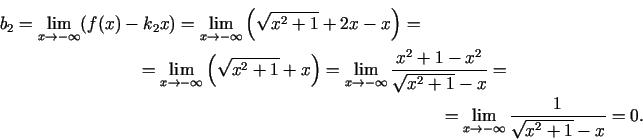
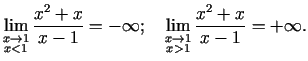
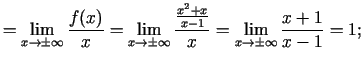
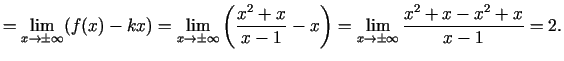
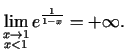
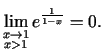
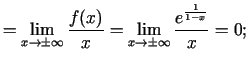
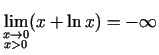 .
.