Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.8. Funkcijas grafika asimptotas
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3.6. Funkcijas grafika ieliekums un izliekums
3.8. definīcija. Funkcijas  grafika punktu
grafika punktu
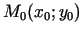 sauc par
tās grafika pārliekuma (infleksijas) punktu, ja
tas atdala grafika izliekto daļu no ieliektās daļas un funkcija
punktā
sauc par
tās grafika pārliekuma (infleksijas) punktu, ja
tas atdala grafika izliekto daļu no ieliektās daļas un funkcija
punktā  ir nepārtraukta.
ir nepārtraukta.
Saskaņā ar šo definīciju punkts 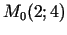 ir funkcijas
ir funkcijas
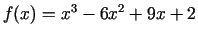 grafika pārliekuma punkts (skat.
3.11. piemēru).
grafika pārliekuma punkts (skat.
3.11. piemēru).
Funkcijas grafiks attēlots 3.3. zīmējumā.
-
3.9. piezīme.
- Pārliekuma punktā
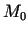 funkcijas grafika
pieskarei no vienas puses jāatrodas virs grafika, bet no otras
puses - zem grafika, t.i., šajā punktā pieskarei ir jākrusto
funkcijas grafiks (3.18. zīm.).
funkcijas grafika
pieskarei no vienas puses jāatrodas virs grafika, bet no otras
puses - zem grafika, t.i., šajā punktā pieskarei ir jākrusto
funkcijas grafiks (3.18. zīm.).
No funkcijas grafika izliekuma un ieliekuma pietiekamā nosacījuma
izriet pārliekuma punkta eksistences nepieciešamais
nosacījums:
ja punkts
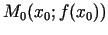 ir funkcijas
ir funkcijas  grafika pārliekuma
punkts, tad
grafika pārliekuma
punkts, tad
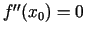 vai arī punktā
vai arī punktā  funkcija nav divreiz
diferencējama.
funkcija nav divreiz
diferencējama.
Formulētais nosacījums nevar būt par funkcijas grafika pārliekuma
punkta pietiekamo nosacījumu. Piemēram, funkcijai 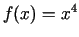 punktā
punktā 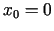
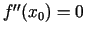 , bet grafika punkts
, bet grafika punkts 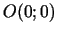 nav tā
pārliekuma punkts.
nav tā
pārliekuma punkts.
3.8. teorēma. (Funkcijas grafika pārliekuma punkta eksistences
pietiekamais nosacījums).
Ja funkcija  ir nepārtraukta punktā
ir nepārtraukta punktā  un, argumentam ejot
caur punktu
un, argumentam ejot
caur punktu  , otrās kārtas atvasinājums
, otrās kārtas atvasinājums 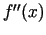 maina zīmi,
tad punkts
maina zīmi,
tad punkts
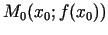 ir funkcijas grafika pārliekuma
punkts.
ir funkcijas grafika pārliekuma
punkts.
Pierādīt
patstāvīgi3.8.
-
3.10. piezīme.
- Ja, argumentam ejot caur
 ,
, 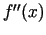 zīme
nemainās, tad punkts ar abscisu
zīme
nemainās, tad punkts ar abscisu  nav funkcijas grafika
pārliekuma punkts.
nav funkcijas grafika
pārliekuma punkts.
Lai atrastu funkcijas grafika pārliekuma punktus, rīkojas šādi.
- Atrod funkcijas otrās kārtas atvasinājumu
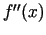 .
.
- Atrod tos punktus, kuros otrās kārtas atvasinājums
ir nulle un arī tos funkcijas
 nepārtrauktības punktus, kuros
šī funkcija nav divreiz diferencējama.
nepārtrauktības punktus, kuros
šī funkcija nav divreiz diferencējama.
- Izpēta otrās kārtas atvasinājuma zīmi šādu punktu apkārtnēs. Ja, argumentam ejot caur kādu no šiem
punktiem
 ,
, 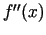 zīme izmainās, tad punkts
zīme izmainās, tad punkts
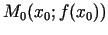 ir funkcijas grafika pārliekuma punkts.
ir funkcijas grafika pārliekuma punkts.
-
3.12. piemērs.
- Atrast funkcijas
![$ f(x)=\sqrt[3]{x^2}+\frac{x^2}{9}$](img793.gif) grafika pārliekuma punktus.
grafika pārliekuma punktus.
- Atradīsim
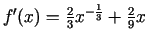 ;
;
- Otrās kārtas atvasinājums ir nulle punktos
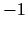 un
un
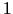 ; punktā 0 otrās kārtas atvasinājums ir bezgalīgs (šajā
punktā funkcija ir nepārtraukta, bet nav divreiz diferencējama).
; punktā 0 otrās kārtas atvasinājums ir bezgalīgs (šajā
punktā funkcija ir nepārtraukta, bet nav divreiz diferencējama).
- Punkti
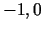 un
un 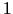 funkcijas definīcijas apgabalu sadala
četros intervālos. Katrā no šiem intervāliem noteiksim
funkcijas definīcijas apgabalu sadala
četros intervālos. Katrā no šiem intervāliem noteiksim 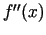 zīmi (3.19. zīm.).
zīmi (3.19. zīm.).
Funkcijas grafika pārliekuma punkti ir
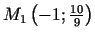 un
un
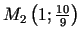 . Funkcijas grafika punktā, kura
abscisa ir 0, pārliekuma nav.
. Funkcijas grafika punktā, kura
abscisa ir 0, pārliekuma nav.
Vienlaicīgi ir atrasti arī funkcijas grafika ieliekuma un
izliekuma intervāli. Funkcijas grafiks ir ieliekts intervālos
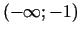 un
un
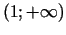 , bet izliekts - intervālā
, bet izliekts - intervālā
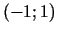 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.8. Funkcijas grafika asimptotas
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3.6. Funkcijas grafika ieliekums un izliekums
2002-01-21
![]() grafika punktu
grafika punktu
![]() sauc par
tās grafika pārliekuma (infleksijas) punktu, ja
tas atdala grafika izliekto daļu no ieliektās daļas un funkcija
punktā
sauc par
tās grafika pārliekuma (infleksijas) punktu, ja
tas atdala grafika izliekto daļu no ieliektās daļas un funkcija
punktā ![]() ir nepārtraukta.
ir nepārtraukta.
![$\displaystyle f''(x)=-\frac{2}{9}x^{-\frac{4}{3}}+\frac{2}{9}=\frac{2}{9}\frac{\sqrt[3]{x^4}-1}{\sqrt[3]{x^4}}\/.$](img795.gif)