


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.7. Funkcijas grafika pārliekuma punkti un
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3.5. Funkcijas vislielākās un vismazākās vērtības
3.7. definīcija. Diferencējamas funkcijas  grafiku
intervālā
grafiku
intervālā  sauc par ieliektu (vai
izliektu), ja tas atrodas virs (vai zem) pieskares, kas
konstruēta grafika jebkurā punktā.
sauc par ieliektu (vai
izliektu), ja tas atrodas virs (vai zem) pieskares, kas
konstruēta grafika jebkurā punktā.
Intervālā  ieliektas funkcijas grafiks attēlots
3.13. zīm., bet izliektas - 3.14. zīm.
ieliektas funkcijas grafiks attēlots
3.13. zīm., bet izliektas - 3.14. zīm.
-
3.7. piezīme.
- Vienas un tās pašas funkcijas grafiks
kādā intervālā var būt izliekts, bet citā intervālā - ieliekts.
Piemēram, funkcijas
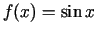 grafiks ir izliekts intervālā
grafiks ir izliekts intervālā
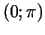 un ieliekts intervālā
un ieliekts intervālā
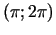 (3.15. zīm.).
(3.15. zīm.).
3.7. teorēma. (Funkcijas grafika ieliekuma pietiekamais
nosacījums).
Ja funkcijai  intervālā
intervālā  eksistē otrās kārtas
atvasinājums un visos intervāla punktos
eksistē otrās kārtas
atvasinājums un visos intervāla punktos 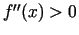 , tad funkcijas
grafiks šajā intervālā ir ieliekts.
, tad funkcijas
grafiks šajā intervālā ir ieliekts.
 Tā kā funkcija ir divas reizes diferencējama
intervālā
Tā kā funkcija ir divas reizes diferencējama
intervālā  , tad šajā intervālā tā ir diferencējama un tāpēc
funkcijas grafika katrā punktā eksistē pieskare.
Izvēlēsimies patvaļīgu
, tad šajā intervālā tā ir diferencējama un tāpēc
funkcijas grafika katrā punktā eksistē pieskare.
Izvēlēsimies patvaļīgu
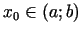 (3.16. zīm.) un
grafika atbilstošajā punktā
(3.16. zīm.) un
grafika atbilstošajā punktā
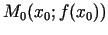 konstruēsim
pieskari, kuras vienādojums ir
konstruēsim
pieskari, kuras vienādojums ir
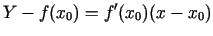 |
(3.1) |
(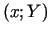 - pieskares punktu koordinātas).
- pieskares punktu koordinātas).
Funkcijai  punkta
punkta  apkārtnē uzrakstīsim Teilora formulu ar
atlikuma locekli Lagranža formā, izvēloties
apkārtnē uzrakstīsim Teilora formulu ar
atlikuma locekli Lagranža formā, izvēloties 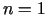 . Iegūsim
. Iegūsim
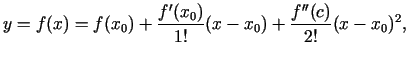 |
(3.2) |
kur 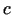 atrodas starp
atrodas starp  un
un  . (
. (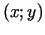 - funkcijas grafika
punktu koordinātas).
- funkcijas grafika
punktu koordinātas).
No vienādības (3.2) atņemsim vienādību
(3.1). Iegūsim
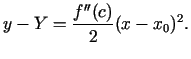 |
(3.3) |
Tā kā intervālā  ir spēkā
ir spēkā 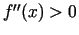 , tad arī
, tad arī 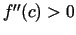 .
Tātad visiem
.
Tātad visiem 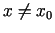 ir spēkā
ir spēkā 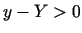 jeb
jeb 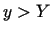 . Tas nozīmē,
ka funkcijas grafiks atrodas virs tā patvaļīgajā punktā
konstruētās pieskares. Tādējādi funkcijas
. Tas nozīmē,
ka funkcijas grafiks atrodas virs tā patvaļīgajā punktā
konstruētās pieskares. Tādējādi funkcijas  grafiks intervālā
grafiks intervālā
 ir ieliekts.
ir ieliekts.
Analogi var formulēt un pierādīt funkcijas grafika izliekuma
pietiekamo nosacījumu.
-
3.8. piezīme.
- Ja atsevišķos punktos
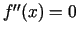 , bet
pārējos intervāla
, bet
pārējos intervāla  punktos
punktos 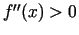 , tad funkcijas
grafiks šajā intervālā ir ieliekts.
, tad funkcijas
grafiks šajā intervālā ir ieliekts.
Lai atrastu funkcijas grafika ieliekuma un izliekuma intervālus,
rīkojas šādi.
- Atrod funkcijas otrās kārtas atvasinājumu
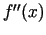 .
.
- Atrod tos intervālus, kuros
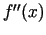 saglabā zīmi.
Ja kādā intervālā
saglabā zīmi.
Ja kādā intervālā 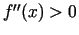 , tad šajā intervālā funkcijas grafiks
ir ieliekts, ja turpretim
, tad šajā intervālā funkcijas grafiks
ir ieliekts, ja turpretim 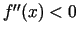 , tad - izliekts.
, tad - izliekts.
-
3.11. piemērs.
- Atrast funkcijas
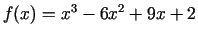 grafika ieliekuma
un izliekuma intervālus.
grafika ieliekuma
un izliekuma intervālus.
- Atrodam
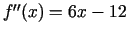 .
.
- Otrās kārtas atvasinājums, acīmredzot, ir
nulle punktā
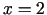 . Šis punkts funkcijas definīcijas apgabalu
sadala divos intervālos. Katrā no šiem intervāliem
. Šis punkts funkcijas definīcijas apgabalu
sadala divos intervālos. Katrā no šiem intervāliem 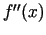 saglabā savu zīmi. Otrās kārtas atvasinājuma zīmes ir lietderīgi
atzīmēt uz skaitļu taisnes (3.17. zīm.).
saglabā savu zīmi. Otrās kārtas atvasinājuma zīmes ir lietderīgi
atzīmēt uz skaitļu taisnes (3.17. zīm.).
Tādējādi funkcijas grafiks intervālā
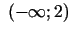 ir
izliekts, bet intervālā
ir
izliekts, bet intervālā
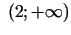 - ieliekts. (Izliekts
funkcijas grafiks apzīmēts ar simbolu
- ieliekts. (Izliekts
funkcijas grafiks apzīmēts ar simbolu 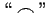 , bet ieliekts -
ar
, bet ieliekts -
ar 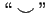 ).
).
Funkcijas grafiks attēlots 3.3. zīmējumā.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.7. Funkcijas grafika pārliekuma punkti un
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3.5. Funkcijas vislielākās un vismazākās vērtības
2002-01-21
![]() grafiku
intervālā
grafiku
intervālā ![]() sauc par ieliektu (vai
izliektu), ja tas atrodas virs (vai zem) pieskares, kas
konstruēta grafika jebkurā punktā.
sauc par ieliektu (vai
izliektu), ja tas atrodas virs (vai zem) pieskares, kas
konstruēta grafika jebkurā punktā.