


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.6. Funkcijas grafika ieliekums un izliekums
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3.4. Funkcijas ekstrēma pietiekamie nosacījumi
Apskatīsim slēgtā intervālā ![$ [a;b]$](img437.gif) nepārtrauktu funkciju
nepārtrauktu funkciju  .
Saskaņā ar Veierštrāsa II teorēmu tā sasniedz šajā intervālā savu
vismazāko un vislielāko vērtību. Šīs vērtības funkcija sasniedz
ekstrēma punktos vai intervāla galapunktos. Lai atrastu funkcijas
vismazāko un vislielāko v
.
Saskaņā ar Veierštrāsa II teorēmu tā sasniedz šajā intervālā savu
vismazāko un vislielāko vērtību. Šīs vērtības funkcija sasniedz
ekstrēma punktos vai intervāla galapunktos. Lai atrastu funkcijas
vismazāko un vislielāko v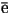 rtību, nav obligāti noteikt ekstrēma
punktus, pietiek atrast funkcijas kritiskos punktus.
rtību, nav obligāti noteikt ekstrēma
punktus, pietiek atrast funkcijas kritiskos punktus.
Lai slēgtā intervālā ![$ [a;b]$](img437.gif) atrastu nepārtrauktas funkcijas
atrastu nepārtrauktas funkcijas  vislielāko un vismazāko vērtību, ir jāizdara šādas darbības.
vislielāko un vismazāko vērtību, ir jāizdara šādas darbības.
- Jāatrod šīs funkcijas visi kritiskie punkti, kas
atrodas intervālā
![$ [a;b]$](img437.gif) .
.
- Jāaprēķina funkcijas vērtības kritiskajos
punktos.
- Jāaprēķina funkcijas vērtības
intervāla galapunktos.
- No iegūtajām vērtībām jāizraugās
vislielākais un vismazākais skaitlis.
-
3.5. piezīme.
- Funkcijas vislielāko vērtību
intervālā
![$ [a;b]$](img437.gif) apzīmē
apzīmē
![$ \max\limits_{[a;b]}f(x)$](img715.gif) , bet vismazāko
vērtību -
, bet vismazāko
vērtību -
![$ \min\limits_{[a;b]}f(x)$](img716.gif) .
.
-
3.7. piemērs.
- Atrast funkcijas
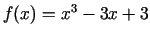 vislielāko un
vismazāko vērtību intervālā
vislielāko un
vismazāko vērtību intervālā ![$ [0;2]$](img718.gif) .
.
- Atrodam
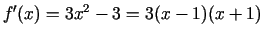 .
.
Kritiskie punkti ir 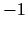 un
un 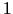 . Intervālam
. Intervālam ![$ [0;2]$](img718.gif) pieder tikai
viens kritiskais punkts
pieder tikai
viens kritiskais punkts 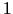 .
.
- Izskaitļojam
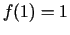 .
.
- Izskaitļojam
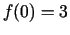 un
un 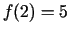 .
.
-
![$ \min\limits_{[0;2]}f(x)=f(1)=1,\quad \max\limits_{[0;2]}f(x)=f(2)=5 $](img724.gif) .
.
-
3.6. piezīme.
-

- Ja funkcija ir nepārtraukta vaļējā
intervālā, tad vismazāko vai vislielāko vērtību tā šajā intervālā
var arī nesasniegt.
- Ja funkcija ir nepārtraukta vaļējā
intervālā un šajā intervālā tai ir vienīgais ekstrēma punkts, tad
šajā punktā funkcija sasniedz vismazāko vērtību, ja tas ir
minimuma punkts, un vislielāko vērtību, ja tas ir maksimuma
punkts.
-
3.8. piemērs.
- Atrast funkcijas
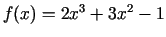 vislielāko un
vismazāko vērtību intervālā
vislielāko un
vismazāko vērtību intervālā 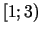 .
.
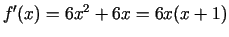 .
.
Kritiskie punkti 0 un 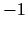 nepieder šim intervālam. Atliek
izskaitļot tikai
nepieder šim intervālam. Atliek
izskaitļot tikai 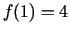 . Acīmredzami funkcija ir augoša
intervālā, jo
. Acīmredzami funkcija ir augoša
intervālā, jo 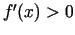 .
.
Tāpēc
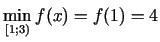 . Vislielāko vērtību
funkcija šajā intervālā nesasniedz.
. Vislielāko vērtību
funkcija šajā intervālā nesasniedz.
-
3.9. piemērs.
- Taisnstūrveida zemes gabala viena mala piekļaujas fabrikas sienai (3.12. zīm.). Ar
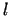 metru garu
stieples gabalu ir jānorobežo šis zemes gabals tā, lai
norobežotajam taisnstūrim būtu iespējami lielāks laukums.
metru garu
stieples gabalu ir jānorobežo šis zemes gabals tā, lai
norobežotajam taisnstūrim būtu iespējami lielāks laukums.
Ja taisnstūra vienas malas garumu apzīmē ar
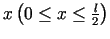 , tad otras malas garums ir
, tad otras malas garums ir 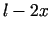 . Taisnstūra
laukums
. Taisnstūra
laukums
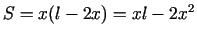 . Jāatrod funkcijas
. Jāatrod funkcijas
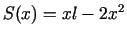 vislielākā vērtība intervālā
vislielākā vērtība intervālā
![$ \left[0;\frac{l}{2}\right]$](img736.gif) .
.
-
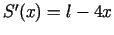 . Kritiskais punkts ir
. Kritiskais punkts ir
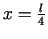 un tas
pieder intervālam
un tas
pieder intervālam
![$ \left[0;\frac{l}{2}\right]$](img736.gif) .
.
- Izskaitļojam
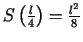 .
.
- Izskaitļojam
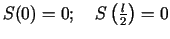 .
.
-
![$ \max\limits_{\left[0;\frac{l}{2}\right]}S(x)=S\left(\frac{l}{4}\right)=\frac{l^2}{8}$](img741.gif) .
.
Taisnstūra malas ir
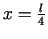 un
un
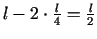 metrus garas.
metrus garas.
-
3.10. piemērs.
- Jāizgatavo cilindriskas formas slēgta tvertne,
kuras tilpums ir
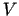 . Jānosaka tvertnes izmēri, lai materiāla
patēriņš būtu mazākais.
. Jānosaka tvertnes izmēri, lai materiāla
patēriņš būtu mazākais.
Apzīmēsim tvertnes rādiusu ar 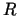 un augstumu ar
un augstumu ar 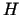 . Tā kā
cilindra tilpums ir
. Tā kā
cilindra tilpums ir
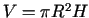 , tad varam izteikt
, tad varam izteikt
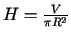 un ievietot cilindra pilnās virsmas formulā
un ievietot cilindra pilnās virsmas formulā
Iegūsim
Jāatrod funkcijas
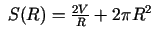 vismazākā
vērtība intervālā
vismazākā
vērtība intervālā
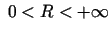 .
.
Vienīgais kritiskais punkts
![$ R=\sqrt[3]{\frac{V}{2\pi}}$](img753.gif) pieder
šim intervālam. Atrodam
pieder
šim intervālam. Atrodam
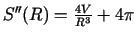 un novērtējam
tā zīmi kritiskajā punktā
un novērtējam
tā zīmi kritiskajā punktā
![$ R=\sqrt[3]{\frac{V}{2\pi}}$](img753.gif) .
Acīmredzami
.
Acīmredzami
![$ S''\left(\sqrt[3]{\frac{V}{2\pi}}\right)>0$](img755.gif) , tāpēc
punktā
, tāpēc
punktā
![$ S=\sqrt[3]{\frac{V}{2\pi}}$](img756.gif) funkcijai
funkcijai 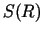 ir minimums.
Šis punkts ir vienīgais ekstrēma punkts vaļējā intervālā
ir minimums.
Šis punkts ir vienīgais ekstrēma punkts vaļējā intervālā
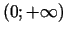 , tāpēc funkcija šajā punktā sasniedz vismazāko
vērtību.
, tāpēc funkcija šajā punktā sasniedz vismazāko
vērtību.
Atrodam
Tvertnei ir jābūt tādai, lai izpildītos nosacījums 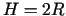 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.6. Funkcijas grafika ieliekums un izliekums
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3.4. Funkcijas ekstrēma pietiekamie nosacījumi
2002-01-21
![$ \max\limits_{\left[0;\frac{l}{2}\right]}S(x)=S\left(\frac{l}{4}\right)=\frac{l^2}{8}$](img741.gif) .
.
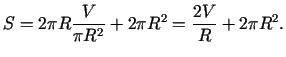
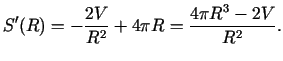
![$ R=\sqrt[3]{\frac{V}{2\pi}}$](img753.gif) pieder
šim intervālam. Atrodam
pieder
šim intervālam. Atrodam
![$ R=\sqrt[3]{\frac{V}{2\pi}}$](img753.gif) .
Acīmredzami
.
Acīmredzami
![$ S''\left(\sqrt[3]{\frac{V}{2\pi}}\right)>0$](img755.gif) , tāpēc
punktā
, tāpēc
punktā
![$ S=\sqrt[3]{\frac{V}{2\pi}}$](img756.gif) funkcijai
funkcijai ![$\displaystyle H=\frac{V}{\pi\left(\sqrt[3]{\frac{V}{2\pi}}\right)^2}=2\sqrt[3]{\frac{V}{2\pi}}\/.$](img759.gif)