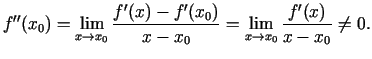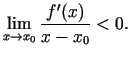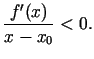Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.5. Funkcijas vislielākās un vismazākās vērtības
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3.3. Funkcijas ekstrēmi un to nepieciešamais
3.5. teorēma. (Funkcijas ekstrēma pietiekamais nosacījums,
izmantojot pirmās kārtas atvasinājumu).
Ja funkcija  ir nepārtraukta punktā
ir nepārtraukta punktā  , ir diferencējama šī
punkta kaut kādā apkārtnē, izņemot varbūt pašu šo punktu, un tās
atvasinājums, argumentam ejot caur punktu
, ir diferencējama šī
punkta kaut kādā apkārtnē, izņemot varbūt pašu šo punktu, un tās
atvasinājums, argumentam ejot caur punktu  , maina
savu zīmi, tad
, maina
savu zīmi, tad  ir funkcijas ekstrēma punkts. Pie tam, ja
atvasinājums pa kreisi no
ir funkcijas ekstrēma punkts. Pie tam, ja
atvasinājums pa kreisi no  ir pozitīvs, pa labi - negatīvs,
tad
ir pozitīvs, pa labi - negatīvs,
tad  ir funkcijas maksimuma punkts, bet, ja atvasinājums pa
kreisi no
ir funkcijas maksimuma punkts, bet, ja atvasinājums pa
kreisi no  ir negatīvs, pa labi - pozitīvs, tad
ir negatīvs, pa labi - pozitīvs, tad  ir
funkcijas minimuma punkts.
ir
funkcijas minimuma punkts.
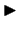 Pieņemsim, ka funkcijas atvasinājums pa
kreisi no
Pieņemsim, ka funkcijas atvasinājums pa
kreisi no  ir pozitīvs. Tas nozīmē, ka pa kreisi no
ir pozitīvs. Tas nozīmē, ka pa kreisi no  funkcija ir augoša. Tāpēc visiem
funkcija ir augoša. Tāpēc visiem 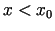 (un kas pieder
(un kas pieder  minētajai apkārtnei)
minētajai apkārtnei)
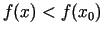 . Pa labi no
. Pa labi no  funkcijas
atvasinājums ir negatīvs. Tāpēc šeit funkcija ir dilstoša un
funkcijas
atvasinājums ir negatīvs. Tāpēc šeit funkcija ir dilstoša un
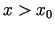 (un kas pieder
(un kas pieder  minētajai apkārtnei)
minētajai apkārtnei)
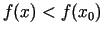 .
Tādējādi
.
Tādējādi  ir funkcijas maksimuma punkts (3.5. zīm.).
Analogi apskata otru gadījumu, kad argumentam ejot caur
ir funkcijas maksimuma punkts (3.5. zīm.).
Analogi apskata otru gadījumu, kad argumentam ejot caur  (argumenta augšanas ``virzienā"), atvasinājums maina zīmi no
(argumenta augšanas ``virzienā"), atvasinājums maina zīmi no
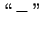 uz
uz 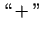 (3.6. zīm.).
(3.6. zīm.).
-
3.3. piezīme.
- Ja, argumentam ejot caur kritisko punktu
 ,
atvasinājums zīmi nemaina, tad
,
atvasinājums zīmi nemaina, tad  nav funkcijas ekstrēma
punkts.
nav funkcijas ekstrēma
punkts.
Formulēsim šādu kārtulu (funkcijas ekstrēma noteikšanas pirmā
kārtula).
Lai atrastu funkcijas ekstrēmus, ir jāveic šādas darbības.
- Jāatrod funkcijas kritiskie punkti.
- Jāizpēta atvasinājuma zīme kritisko punktu
apkārtnēs. Ja, argumentam ejot caur kādu kritisko punktu,
atvasinājuma zīme mainās no
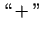 uz
uz 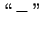 , tad šajā punktā
funkcijai ir maksimums, bet, ja atvasinājuma zīme mainās no
, tad šajā punktā
funkcijai ir maksimums, bet, ja atvasinājuma zīme mainās no 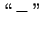 uz
uz 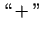 , tad - minimums. Ja atvasinājuma zīme nemainās, tad
funkcijai šajā punktā ekstrēma nav.
, tad - minimums. Ja atvasinājuma zīme nemainās, tad
funkcijai šajā punktā ekstrēma nav.
- Jāprēķina funkcijas vērtības ekstrēmu
punktos.
-
3.3. piemērs.
- Atrast funkcijas
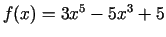 ekstrēmus.
ekstrēmus.
- Lai atrastu funkcijas kritiskos punktus, atradīsim
Kritiskie punkti (šoreiz stacionārie punkti) ir
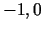 un
un 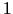 .
.
- Atvasinājuma vērtību zīmes atzīmēsim
uz skaitļu taisnes (3.7. zīm.).
Funkcijas maksimuma punkts ir
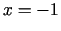 , bet minimuma punkts ir
, bet minimuma punkts ir
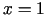 . Punktā
. Punktā 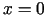 ekstrēma nav.
ekstrēma nav.
- Aprēķināsim funkcijas vērtības
ekstrēmu punktos.
Vienlaicīgi esam noteikuši arī funkcijas monotonitātes intervālus.
Augšanas intervāli ir
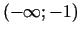 un
un
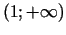 , bet
dilšanas intervāls -
, bet
dilšanas intervāls - 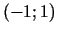 . Funkcijas grafiks attēlots
3.8. zīmējumā.
. Funkcijas grafiks attēlots
3.8. zīmējumā.
-
3.4. piemērs.
- Atrast funkcijas
![$ f(x)=x-3\sqrt[3]{x}$](img682.gif) ekstrēmus.
ekstrēmus.
-
![$ f'(x)=1-3\cdot\frac{1}{3}x^{-\frac{2}{3}}=
1-\frac{1}{\sqrt[3]{x^2}}=\frac{\sqrt[3]{x^2}-1}{\sqrt[3]{x^2}}$](img683.gif) .
Kritiskie punkti ir
.
Kritiskie punkti ir 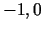 un
un 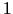 .
.
- Atvasinājuma vērtību zīmes atzīmēsim
uz skaitļu taisnes (3.9. zīm.). Punktā
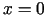 funkcija nav
diferencējama.
funkcija nav
diferencējama.
Funkcijas maksimuma punkts ir 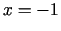 , bet minimuma punkts ir
, bet minimuma punkts ir
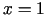 . Punktā
. Punktā 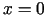 ekstrēma nav.
ekstrēma nav.
-
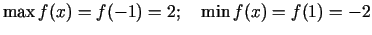 .
.
Funkcija aug intervālos
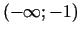 un
un
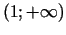 , bet dilst
intervālā
, bet dilst
intervālā 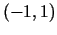 . Funkcijas grafiks attēlots
3.10. zīmējumā.
. Funkcijas grafiks attēlots
3.10. zīmējumā.
-
3.5. piemērs.
- Atrast funkcijas
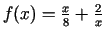 ekstrēmus.
ekstrēmus.
Funkcija nav definēta punktā 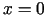 .
.
-
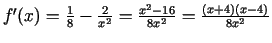 .
.
Kritiskie punkti ir 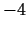 un
un 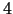 . (Punkts
. (Punkts 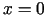 nevar būt par
kritisko punktu, jo tas nepieder funkcijas definīcijas apgabalam).
nevar būt par
kritisko punktu, jo tas nepieder funkcijas definīcijas apgabalam).
- Uz skaitļu taisnes atzīmēsim atvasinājumu
vērtību zīmes (uz skaitļu taisnes ir jātzīmē arī punkts
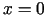 )
(3.11. zīm.).
)
(3.11. zīm.).
Funkcijas maksimuma punkts ir 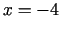 , bet minimuma punkts
ir
, bet minimuma punkts
ir 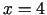 .
.
-
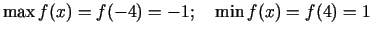 .
.
Funkcija aug intervālos
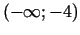 un
un
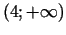 , bet dilst intervālos
, bet dilst intervālos 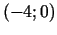 un
un 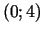 .
.
3.6. teorēma. (Funkcijas ekstrēma pietiekamais nosacījums,
izmantojot otrās kārtas atvasinājumu).
Ja funkcija  ir diferencējama stacionāra punkta
ir diferencējama stacionāra punkta  apkārtnē
un šajā punktā eksistē galīgs
apkārtnē
un šajā punktā eksistē galīgs
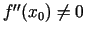 , tad
, tad  ir
funkcijas ekstrēma punkts. Pie tam, ja
ir
funkcijas ekstrēma punkts. Pie tam, ja
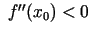 , tad
, tad 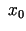 ir maksimuma punkts, bet, ja
ir maksimuma punkts, bet, ja
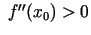 , tad - minimuma
punkts.
, tad - minimuma
punkts.
 Tā kā
Tā kā  ir funkcijas stacionārais
punkts, tad
ir funkcijas stacionārais
punkts, tad 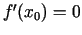 . Punktā
. Punktā  eksistē
eksistē
Pieņemsim, ka
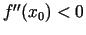 jeb
jeb
Punkta  kaut kādā apkārtnē funkcija saglabā savas robežas
zīmi, t.i.,
kaut kādā apkārtnē funkcija saglabā savas robežas
zīmi, t.i.,
No šīs nevienādības seko, ka visiem 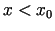 (un kas pieder
minētajai apkārtnei)
(un kas pieder
minētajai apkārtnei) 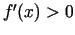 , bet
, bet 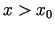 izpildās
izpildās 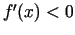 .
Tādējādi, argumentam ejot caur punktu
.
Tādējādi, argumentam ejot caur punktu  , atvasinājums maina
zīmi no
, atvasinājums maina
zīmi no 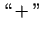 uz
uz 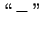 . Punkts
. Punkts  ir funkcijas maksimuma
punkts.
ir funkcijas maksimuma
punkts.
Analogi apskata gadījumu, kad
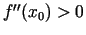 .
.
-
3.4. piezīme.
- Izmantojot otrās kārtas atvasinājumu, uz
ekstrēmu drīkst pētīt tikai funkcijas stacionāros punktus. Pie tam
šis nosacījums nav pielietojams tajos stacionārajos punktos, kuros
otrās kārtas atvasinājums ir nulle, bezgalība vai vispār
neeksistē. Šādos gadījumos ir jālieto pirmā kārtula.
Formulēsim funkcijas ekstrēma noteikšanas otro kārtulu.
Lai atrastu funkcijas ekstrēmus, ir jāveic šādas darbības.
- Jāatrod funkcijas stacionārie punkti.
- Jāatrod
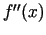 un jānosaka tā skaitliskā
vērtība katrā stacionārajā punktā
un jānosaka tā skaitliskā
vērtība katrā stacionārajā punktā  (protams, ja tāda
eksistē). Ja
(protams, ja tāda
eksistē). Ja
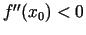 , tad
, tad  ir maksimuma punkts, bet ja
ir maksimuma punkts, bet ja
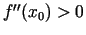 , tad
, tad  - minimuma punkts.
- minimuma punkts.
- Jāaprēķina funkcijas vērtības
ekstrēma punktos.
-
3.6. piemērs.
- Atrast funkcijas
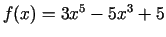 ekstrēmus.
ekstrēmus.
-
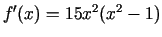 . Stacionārie punkti ir
. Stacionārie punkti ir 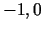 un
un 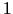 .
.
-
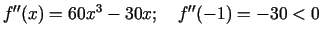 . Punkts
. Punkts 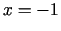 ir
funkcijas maksimuma punkts.
ir
funkcijas maksimuma punkts. 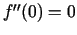 . Otrā kārtula šī punkta
raksturu nenosaka. Punkts
. Otrā kārtula šī punkta
raksturu nenosaka. Punkts 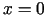 nav funkcijas ekstrēma punkts
(skat. 3.3. piemēru).
nav funkcijas ekstrēma punkts
(skat. 3.3. piemēru).
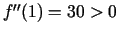 . Punkts
. Punkts 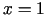 ir
funkcijas minimuma punkts.
ir
funkcijas minimuma punkts.
-
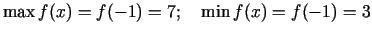 .
.
Funkcijas grafiks attēlots 3.8. zīmējumā.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.5. Funkcijas vislielākās un vismazākās vērtības
Augstāk: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Iepriekšējais: 3.3. Funkcijas ekstrēmi un to nepieciešamais
2002-01-21
![\includegraphics[width=11cm]{C:/TEXfiles/vitolds/fun_lv_html/16arma.eps}](img669.gif)