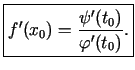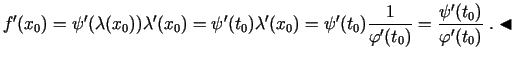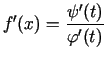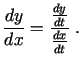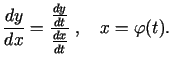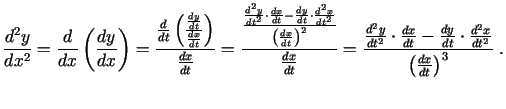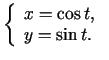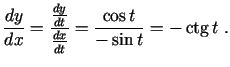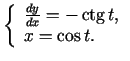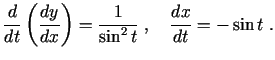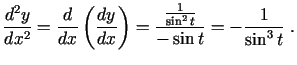Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.2. Līniju parametriskie vienādojumi
Augstāk: 4. PARAMETRISKI UZDOTAS FUNKCIJAS UN VEKTORFUNKCIJAS
Iepriekšējais: 4. PARAMETRISKI UZDOTAS FUNKCIJAS UN VEKTORFUNKCIJAS
Apskatīsim divas funkcijas
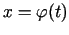 un
un 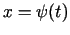 , kas
definētas kaut kādā intervālā
, kas
definētas kaut kādā intervālā 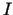 . Ja, piemēram, funkcija
. Ja, piemēram, funkcija
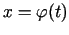 ir stingri monotona šajā intervālā, tad tai
eksistē apvērstā funkcija
ir stingri monotona šajā intervālā, tad tai
eksistē apvērstā funkcija
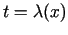 , kas definēta
atbilstošajā kopā
, kas definēta
atbilstošajā kopā
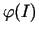 . Izveidosim saliktu funkciju
. Izveidosim saliktu funkciju
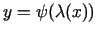 , kas definēta kopā
, kas definēta kopā
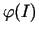 un kas izsaka
un kas izsaka
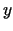 kā argumenta
kā argumenta  funkciju.
funkciju.
Pāreju no vienādojumiem
uz vienādojumu
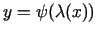 sauc par parametra
sauc par parametra 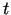 izslēgšanu.
izslēgšanu.
Parametra izslēgšana ne tik vien nav nepieciešama, bet bieži vien
praktiski nav iespējama. Tāpēc parasti parametru neizslēdz un
saka, ka argumenta  funkcija
funkcija
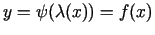 ir
uzdota parametriski ar vienādojumiem
ir
uzdota parametriski ar vienādojumiem
(parametrs 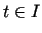 ).
).
Noskaidrosim, kā, neizslēdzot parametru, atrast parametriski
uzdotas funkcijas atvasinājumus.
4.1. teorēma. Ja funkcijas
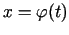 un
un
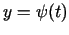 ir definētas intervālā
ir definētas intervālā  , ir diferencējamas
punktā
, ir diferencējamas
punktā
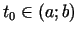 , pie tam
, pie tam
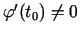 ; funkcija
; funkcija
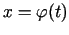 ir stingri monotona un nepārtraukta, tad funkcija
ir stingri monotona un nepārtraukta, tad funkcija
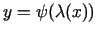 ir diferencējama punktā
ir diferencējama punktā
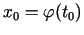 ,
pie tam
,
pie tam
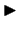 Saskaņā ar 1.8. teorēmu (par
apvērstas funkcijas atvasināšanu) funkcija
Saskaņā ar 1.8. teorēmu (par
apvērstas funkcijas atvasināšanu) funkcija
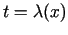 ir
diferencējama punktā
ir
diferencējama punktā
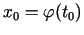 , pie tam
, pie tam
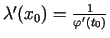 .
.
Saskaņā ar 1.7. teorēmu (par saliktas funkcijas
atvasināšanu) funkcija
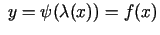 ir
diferencējama punktā
ir
diferencējama punktā  , pie tam
, pie tam
-
4.1. piezīme.
- Ja 4.1. teorēmas nosacījumi ir
izpildīti intervāla
 katrā punktā
katrā punktā 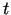 , tad pēc formulas
atrastais atvasinājums, acīmredzot, ir
, tad pēc formulas
atrastais atvasinājums, acīmredzot, ir 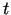 funkcija, kas definēta
šajā intervālā. Šo formulu pieraksta vēl šādā izskatā:
funkcija, kas definēta
šajā intervālā. Šo formulu pieraksta vēl šādā izskatā:
Izmantojot 4.1. teorēmu atkārtoti, var atrast arī
augstāku kārtu atvasinājumus parametriski uzdotām
funkcijām. Parādīsim, kā atrod otrās kārtas atvasinājumu
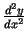 . Var uzskatīt, ka funkcija
. Var uzskatīt, ka funkcija
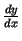 arī
ir uzdota parametriski ar vienādojumiem
arī
ir uzdota parametriski ar vienādojumiem
Šai parametriski uzdotai funkcijai pielietojot 4.1.
teorēmu,4.1 iegūstam
-
4.2. piezīme.
- Praktiski
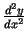 atrašanai šo
formulu lieto reti, bet lieto to paņēmienu, ar kuru tika iegūta šī
formula.
atrašanai šo
formulu lieto reti, bet lieto to paņēmienu, ar kuru tika iegūta šī
formula.
-
4.1. piemērs.
- Atrast
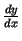 un
un
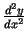 parametriski uzdotai funkcijai
parametriski uzdotai funkcijai
Šīs funkcijas apmierina 4.1. teorēmas nosacījumus
katrā no intervāliem
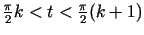 , kur
, kur
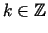 .
.
Katrā no šiem intervāliem var atrast
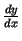 un
un
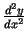 .
.
Tā kā
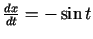 ,
,
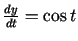 , tad
, tad
Uzrakstīsim sistēmu:
Atrodam
Tādējādi



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.2. Līniju parametriskie vienādojumi
Augstāk: 4. PARAMETRISKI UZDOTAS FUNKCIJAS UN VEKTORFUNKCIJAS
Iepriekšējais: 4. PARAMETRISKI UZDOTAS FUNKCIJAS UN VEKTORFUNKCIJAS
2002-01-21
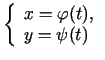
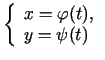
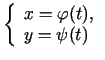
![]() un
un
![]() ir definētas intervālā
ir definētas intervālā ![]() , ir diferencējamas
punktā
, ir diferencējamas
punktā
![]() , pie tam
, pie tam
![]() ; funkcija
; funkcija
![]() ir stingri monotona un nepārtraukta, tad funkcija
ir stingri monotona un nepārtraukta, tad funkcija
![]() ir diferencējama punktā
ir diferencējama punktā
![]() ,
pie tam
,
pie tam