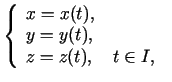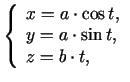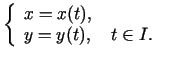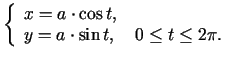Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.3. Reālā argumenta vektorfunkcijas
Augstāk: 4. PARAMETRISKI UZDOTAS FUNKCIJAS UN VEKTORFUNKCIJAS
Iepriekšējais: 4.1. Parametriski uzdotas funkcijas un to
Pieņemsim, ka punkta stāvoklis telpā mainās atkarībā no laika 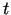 .
Punkta koordinātas
.
Punkta koordinātas  ,
, 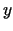 ,
, 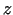 atkarībā no laika izmainās šādi:
atkarībā no laika izmainās šādi:
kur 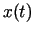 ,
, 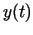 ,
, 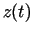 ir kaut kādā intervālā
ir kaut kādā intervālā 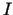 nepārtrauktas funkcijas.
nepārtrauktas funkcijas.
Kustīgais punkts telpā apraksta kaut kādu nepārtrauktu līniju 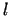 ,
kuru sauc vēl par Žordano loku.4.2
,
kuru sauc vēl par Žordano loku.4.2
4.1. definīcija. Līniju 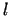 , kuras parametriskais vienādojums ir
, kuras parametriskais vienādojums ir
sauc par gludu, ja funkcijām 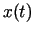 ,
, 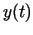 ,
, 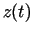 šajā
intervālā eksistē nepārtraukti atvasinājumi.
šajā
intervālā eksistē nepārtraukti atvasinājumi.
Piemēram, skrūves līnijas parametriskais vienādojums ir
(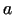 un
un 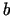 - pozitīvi skaitļi).
- pozitīvi skaitļi).
Plaknes līnijas parametriskais vienādojums ir:
Piemēram, elipses parametriskais vienādojums ir



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.3. Reālā argumenta vektorfunkcijas
Augstāk: 4. PARAMETRISKI UZDOTAS FUNKCIJAS UN VEKTORFUNKCIJAS
Iepriekšējais: 4.1. Parametriski uzdotas funkcijas un to
2002-01-21
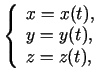
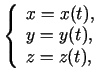
![]() , kuras parametriskais vienādojums ir
, kuras parametriskais vienādojums ir