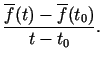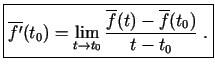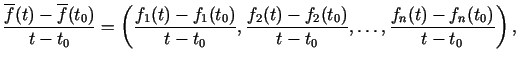Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.4. Jautājumi
Augstāk: 4. PARAMETRISKI UZDOTAS FUNKCIJAS UN VEKTORFUNKCIJAS
Iepriekšējais: 4.2. Līniju parametriskie vienādojumi
Apskatīsim reālā argumenta 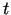 tādu funkciju, kas katrai
tādu funkciju, kas katrai 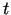 vērtībai no kādas kopas
vērtībai no kādas kopas 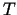 pēc noteikta likuma piekārto telpas
pēc noteikta likuma piekārto telpas
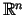 vienu vektoru.
vienu vektoru.
Šādu funkciju sauc par reālā argumenta 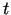 vektorfunkciju un
apzīmē
vektorfunkciju un
apzīmē
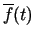 . Šī mainīgā vektora
. Šī mainīgā vektora
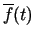 koordinātas ir argumenta
koordinātas ir argumenta 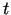 reālas funkcijas:
reālas funkcijas: 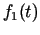 ,
, 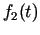 ,
,
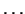 ,
, 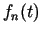 (visas šīs koordinātu funkcijas ir definētas
kopā
(visas šīs koordinātu funkcijas ir definētas
kopā 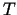 ).
).
Kā zināms, vektoru pilnīgi nosaka tā koordinātas. Tāpēc uzdot
vektorfunkciju
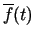 nozīmē uzdot
nozīmē uzdot 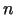 reālas funkcijas
reālas funkcijas
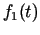 ,
, 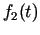 ,
, 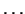 ,
, 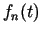 . Vektorfunkciju
. Vektorfunkciju
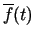 parasti pieraksta šādi:
parasti pieraksta šādi:
jeb
kur
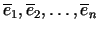 -
koordinātu asu vienības vektori jeb orti.
-
koordinātu asu vienības vektori jeb orti.
Ja izvēlamies noteiktu argumenta vērtību 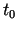 , tad šai vērtībai
atbilst noteikts pastāvīgs (konstants) vektors
, tad šai vērtībai
atbilst noteikts pastāvīgs (konstants) vektors
(Šī vektora koordinātas ir reālie skaitļi).
4.2. definīcija. Par divu vektorfunkciju
un
summu sauc šādu vektorfunkciju
un apzīmē:
4.3. definīcija. Par vektorfunkcijas
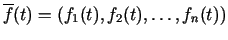 reizinājumu ar reālu skaitli
reizinājumu ar reālu skaitli 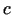 sauc šādu vektorfunkciju
sauc šādu vektorfunkciju
un apzīmē
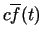 .
.
-
4.3. piezīme.
- Analogi var definēt
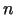 vektorfunkciju lineāro
kombināciju.
vektorfunkciju lineāro
kombināciju.
Apskatīsim vektorfunkciju
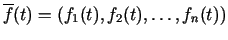 , kas definēta punkta
, kas definēta punkta 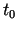 kaut kādā
apkārtnē, izņemot varbūt pašu šo punktu.
kaut kādā
apkārtnē, izņemot varbūt pašu šo punktu.
4.4. definīcija. Pastāvīgu vektoru
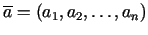 sauc par vektorfunkcijas
sauc par vektorfunkcijas
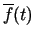 robežu
punktā
robežu
punktā 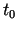 , ja
, ja
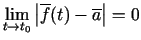 .
.
Pieraksta
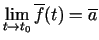 .
.
No divkāršām nevienādībām
seko, ka
4.5. definīcija. Vektorfunkciju
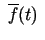 sauc par nepārtrauktu punktā
sauc par nepārtrauktu punktā
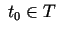 , ja
, ja
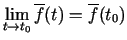 .
.
Ņemot vērā sakarību, kas pastāv starp vektorfunkcijas robežu un
tās koordinātu funkciju robežām, seko, ka vektorfunkcija ir
nepārtraukta punktā 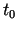 tad un tikai tad, kad šajā punktā ir
nepārtrauktas tās koordinātu funkcijas.
tad un tikai tad, kad šajā punktā ir
nepārtrauktas tās koordinātu funkcijas.
Apskatīsim punkta 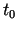 apkārtnē definētu vektorfunkciju
apkārtnē definētu vektorfunkciju
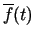 . Punkta
. Punkta 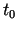 apkārtnē izvēlēsimies patvaļīgu
punktu
apkārtnē izvēlēsimies patvaļīgu
punktu 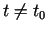 un sastādīsim šādu attiecību
un sastādīsim šādu attiecību
Ja šādai attiecībai punktā 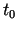 eksistē robeža, tad šo vektoru,
kuru apzīmē
eksistē robeža, tad šo vektoru,
kuru apzīmē
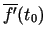 , sauc par vektorfunkcijas atvasinājumu punktā
, sauc par vektorfunkcijas atvasinājumu punktā 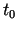 . Pie tam vektorfunkciju
. Pie tam vektorfunkciju
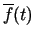 sauc par diferencējamu punktā
sauc par diferencējamu punktā 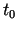 .
.
Tādējādi
Tā kā
tad acīmredzami
jeb



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.4. Jautājumi
Augstāk: 4. PARAMETRISKI UZDOTAS FUNKCIJAS UN VEKTORFUNKCIJAS
Iepriekšējais: 4.2. Līniju parametriskie vienādojumi
2002-01-21
![]() reizinājumu ar reālu skaitli
reizinājumu ar reālu skaitli ![]() sauc šādu vektorfunkciju
sauc šādu vektorfunkciju
![]() sauc par vektorfunkcijas
sauc par vektorfunkcijas
![]() robežu
punktā
robežu
punktā ![]() , ja
, ja
![]() .
.
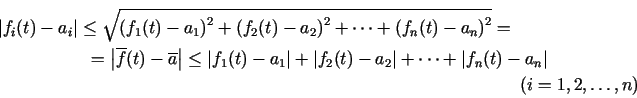
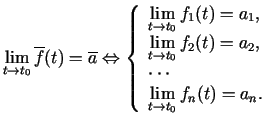
![]() sauc par nepārtrauktu punktā
sauc par nepārtrauktu punktā
![]() , ja
, ja
![]() .
.