


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.9. Uzdevumi
Augstāk: 2.6. Noteiktā integrāļa vispārinājums
Iepriekšējais: 2.7. Jautājumi
- Funkcijai
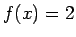 sastādīt integrālsummu intervālā
sastādīt integrālsummu intervālā ![$ [0;6]$](img753.gif) un izskaitļot noteikto integrāli no šīs funkcijas.
un izskaitļot noteikto integrāli no šīs funkcijas.
- Noskaidrot, vai
ir integrējama funkcija intervālā
![$ [0;2]$](img755.gif) . Atbildi pamatot.
. Atbildi pamatot.
- Dotajām funkcijām intervālā
![$ [0;10]$](img756.gif) sastādīt Darbū summas
(veidojot intervāla sasmalcinājumu, par starppunktiem izvēlēties naturālos
skaitļus). Sniegt ģeometrisko interpretāciju.
sastādīt Darbū summas
(veidojot intervāla sasmalcinājumu, par starppunktiem izvēlēties naturālos
skaitļus). Sniegt ģeometrisko interpretāciju.
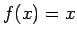 ,
,
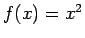 ,
,
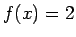 ,
,
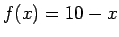 .
.
- Pamatot Darbū summu 1., 4.
un 5. īpašību.
- Pamatot Darbū summu 2. īpašību apakšējai
Darbū summai.
- Pamatot Darbū summu 3. īpašību apakšējām
Darbū summām.
- Sniegt ģeometrisko interpretāciju noteiktā integrāļa 6.,
7., 9.
un 10. īpašībai.
- Pierādīt noteiktā integrāļa 2.
un 7. īpašību.
- Pamatot, ka
kur
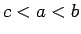 .
.
- Neizskaitļojot integrāļus, noteikt to zīmi:
-
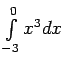 ,
,
-
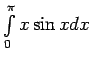 .
.
- Neizskaitļojot integrāļus, noteikt, kuram no tiem ir lielāka
vērtība:
-
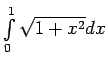 vai
vai
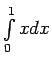 ,
,
-
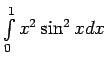 vai
vai
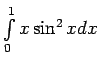 ,
,
-
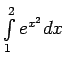 vai
vai
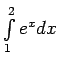 .
.
- Aprēķināt šādu funkciju vidējo vērtību2.7 norādītajā intervālā:
-
![$ f(x)=x,\quad[0;1]$](img771.gif) ,
,
-
![$ f(x)=1+x,\quad[1;10]$](img772.gif) ,
,
-
![$ f(x)=x^2,\quad[0;a]$](img773.gif) .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.9. Uzdevumi
Augstāk: 2.6. Noteiktā integrāļa vispārinājums
Iepriekšējais: 2.7. Jautājumi
2002-11-06
![$\displaystyle f(x)=\left\{\begin{array}{cl}
-1, & \text{ja}\;x \text{ ir interv...
... \;\text{ir intervāla}\;[0;2]\;\text{iracionāls skaitlis} \
\end{array}\right.$](img754.gif)
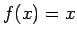 ,
,
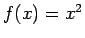 ,
,
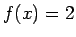 ,
,
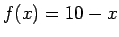 .
.
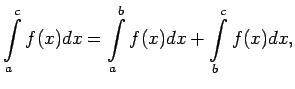
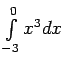 ,
,
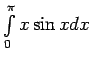 .
.
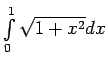 vai
vai
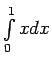 ,
,
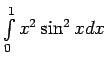 vai
vai
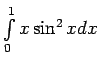 ,
,
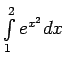 vai
vai
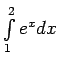 .
.
![$ f(x)=x,\quad[0;1]$](img771.gif) ,
,
![$ f(x)=1+x,\quad[1;10]$](img772.gif) ,
,
![$ f(x)=x^2,\quad[0;a]$](img773.gif) .
.
![$\displaystyle f(x)=\left\{\begin{array}{cl}
-1, & \text{ja}\;x \text{ ir interv...
... \;\text{ir intervāla}\;[0;2]\;\text{iracionāls skaitlis} \
\end{array}\right.$](img754.gif)
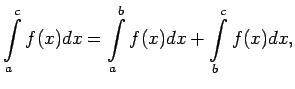
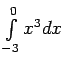 ,
,
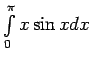 .
.
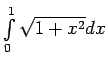 vai
vai
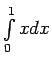 ,
,
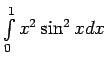 vai
vai
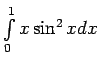 ,
,
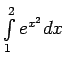 vai
vai
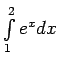 .
.