- ... funkcija?1.1
- Apskatīt
funkciju
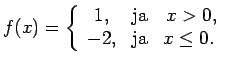
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Darbū2.1
- G. Darbū (1842-1917) -
franču matemātiķis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....2.2
- Pierāda līdzīgi kā
Dirihlē funkcijai.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... patstāvīgi).2.3
- Izveidot intervāla
![$ [a;b]$](img524.gif) sasmalcinājumu, kuram par dalījuma punktiem ir
sasmalcinājumu, kuram par dalījuma punktiem ir 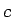 un
un 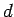 .
Pielietot 2.2. teorēmu.
.
Pielietot 2.2. teorēmu.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... patstāvīgi2.4
- Izmantot noteiktā integrāļa
monotonitātes īpašību un formulu
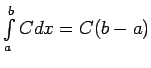 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... laukums2.5
- Līklīnijas
trapeces kvadrējamība tiks pamatota nedaudz vēlāk. Tiks pierādīts,
ka līklīnijas trapeces laukums ir vienāds ar noteikto integrāli
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... integrāļus2.6
- Šos integrāļus viegli viegli varēs izskaitļot
vēlāk, izmantojot Ņūtona-Leibnica formulu.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... vērtību2.7
- Vērtība
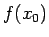 , kas ir
vienāda ar
, kas ir
vienāda ar
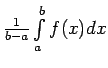 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ierobežotu4.1
- Eksistē tāds riņķis, kas satur kopu
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
laukumu4.2
- No ģeometrijas kursa ir zināms, ka katram plaknes
daudzstūrim atbilst nenegatīvs skaitlis, kuru sauc par šī
daudzstūra laukumu. Plaknes daudzstūra laukumam piemīt šādas
īpašības:
- aditivitāte, t.i., ja
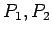 - plaknes
daudzstūri, kuriem nav kopīgu iekšējo punktu, tad
- plaknes
daudzstūri, kuriem nav kopīgu iekšējo punktu, tad
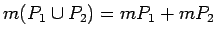 ,
,
- monotonitāte, t.i., ja
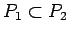 , tad
, tad
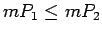 ,
,
- invariance, t.i., ja plaknes daudzstūri
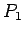 un
un 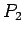 ir
vienādi, tad
ir
vienādi, tad 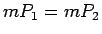 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tukša4.3
- Ja kopa
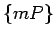 ir
tukša, t.i., plaknes figūrā
ir
tukša, t.i., plaknes figūrā  nevar ievilkt nevienu plaknes
daudzstūri
nevar ievilkt nevienu plaknes
daudzstūri 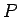 , tad uzskata, ka
, tad uzskata, ka
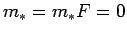 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Ka\-val\-je\-ri5.1
- B. Kavaljeri (1591-1647) - itāļu
matemātiķis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... punkta5.2
- Ģeometrisks punkts,
kurā ir koncentrēta zināma
masa.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
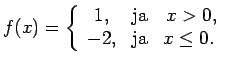
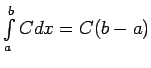 .
.
 .
.
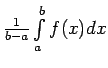 .
.
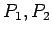 - plaknes
daudzstūri, kuriem nav kopīgu iekšējo punktu, tad
- plaknes
daudzstūri, kuriem nav kopīgu iekšējo punktu, tad
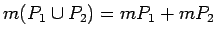 ,
,
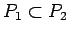 , tad
, tad
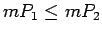 ,
,
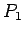 un
un 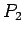 ir
vienādi, tad
ir
vienādi, tad 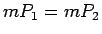 .
.