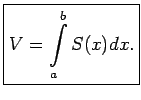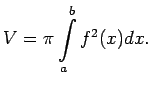Izveido intervāla
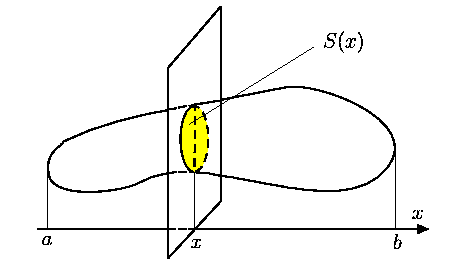
Pieņem, ka ķermeņa daļa starp plaknēm ![]() ,
, ![]() ir taisns
cilindrs, kura pamatā ir figūra ar laukumu
ir taisns
cilindrs, kura pamatā ir figūra ar laukumu ![]() , kur
, kur
![]() un kura augstums ir
un kura augstums ir
![]() .
.
Šīs ķermeņa daļas tilpums aptuveni būs vienāds ar
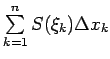 .
.
Lai precīzi raksturotu dotā ķermeņa tilpumu
Šāda robeža eksistē, jo
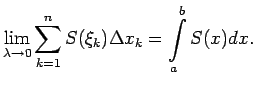
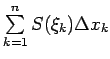 ) ir integrālsumma
funkcijai
) ir integrālsumma
funkcijai Tādējādi
- 5.3. piezīme.
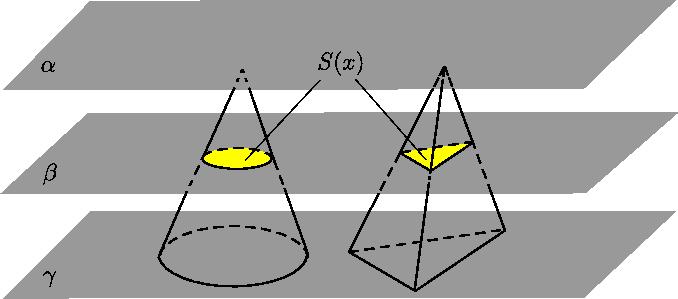
- No formulas (5.7) izriet jau 17. gadsimtā pazīstamais Kavaljeri5.1 princips: ja divi ķermeņi, kas novietoti starp divām paralēlajām plaknēm, šķēlumā ar jebkuru citu tām paralēlu plakni dod vienlielas figūras (vienādi laukumi), tad šie ķermeņi ir vienlieli (tiem ir vienādi tilpumi) (5.12. zīm.).
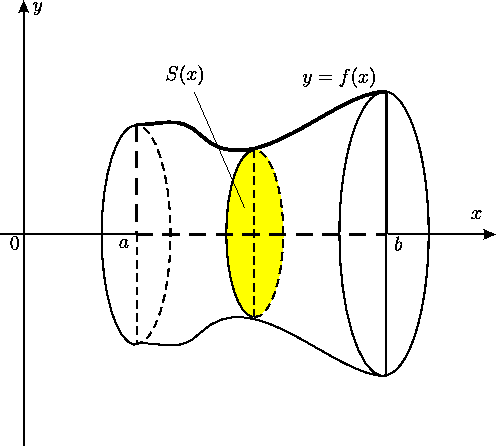
Šādu ķermeni, kuru sauc par rotācijas ķermeni, šķeļot ar
jebkuru abscisu asij perpendikulāru plakni, iegūst riņķi, kura
rādiuss ir ![]() . Tāpēc iegūtā šķērsgriezuma laukums
. Tāpēc iegūtā šķērsgriezuma laukums
![]() .
.
Tādējādi