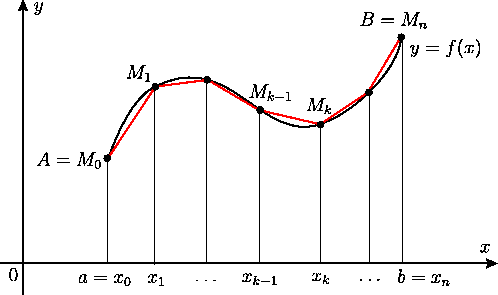
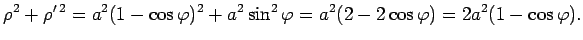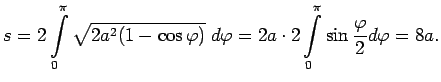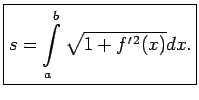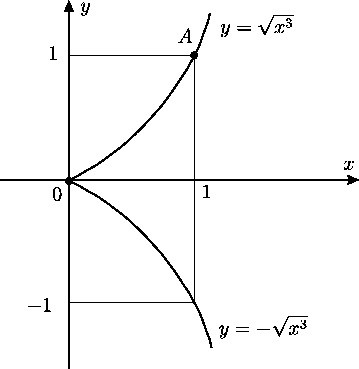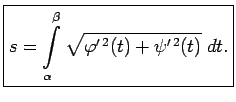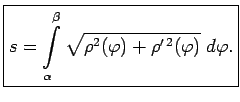Ja izveido līknes
Punkta
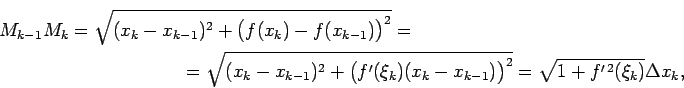
kur
Starpība
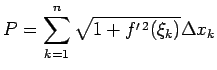
Šī funkcija ir integrējama kā nepārtraukta funkcija, tāpēc integrālsummai eksistē galīga robeža, kad
Robeža ir vienāda ar šādu noteikto integrāli:
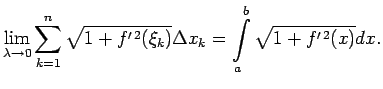
- 5.4. piemērs.
- Aprēķināt puskubiskās parabolas
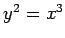 loka garumu
starp punktiem
loka garumu
starp punktiem 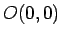 ,
, 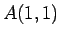 (5.8. zīm.).
(5.8. zīm.).
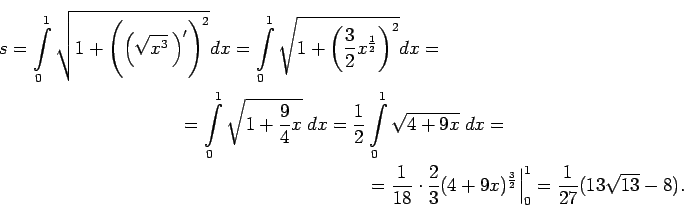
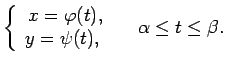
Funkcijas
![]() intervālā
intervālā
![]() ir stingri
monotona un nepārtraukti diferencējama, bet
ir stingri
monotona un nepārtraukti diferencējama, bet ![]() ir
nepārtraukti diferencējama. Ja parametrs
ir
nepārtraukti diferencējama. Ja parametrs ![]() mainās no
mainās no ![]() līdz
līdz ![]() , tad
, tad ![]() mainās no
mainās no ![]() līdz
līdz ![]() .
.
Vienādojumu sistēma
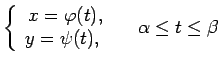
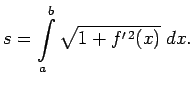
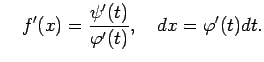
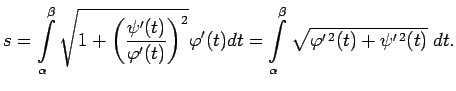
- 5.5. piemērs.
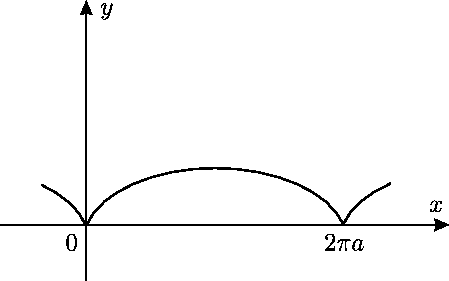
- Aprēķināt cikloīdas
vienas arkas garumu (5.9. zīm.).
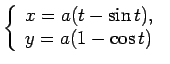
Vienu arku iegūst, parametru
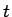 izmainot no 0 līdz
izmainot no 0 līdz 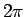 .
.
Tā kā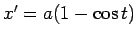 ,
,
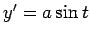 , tad
, tad
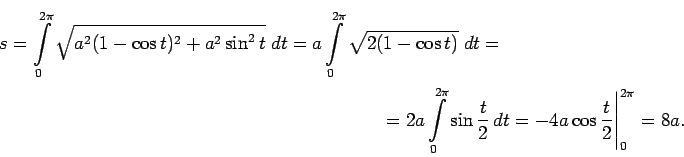
- 5.2. piezīme.
- Formula (5.5) ir spēkā arī tādai
parametriskā veidā uzdotai līknei
kas nav kaut kādas funkcijas grafiks. Svarīgi, lai tikai funkcijas
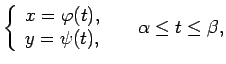
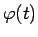 ,
, 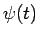 būtu nepārtraukti diferencējamas minētajā
intervālā.
būtu nepārtraukti diferencējamas minētajā
intervālā.
Parametrizē šo līkni
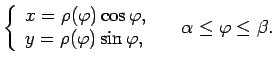
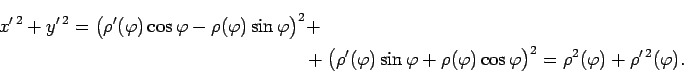
Pielieto formulu (5.5) un iegūst, ka
- 5.6. piemērs.
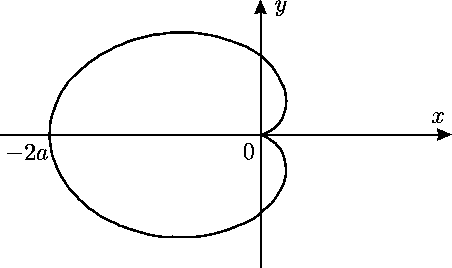
- Aprēķināt kardioīdas
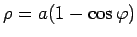 garumu
(skat. 5.10. zīm.).
garumu
(skat. 5.10. zīm.).
Atrod
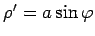 ,
,