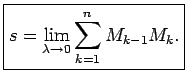Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 5.3. Līknes garuma aprēķināšana ar noteikto
Augstāk: 5. NOTEIKTĀ INTEGRĀĻA LIETOJUMI
Iepriekšējais: 5.1. Laukuma aprēķināšana ar noteikto integrāli
Plaknē apskata līkni 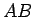 (
(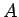 - līknes sākuma, bet
- līknes sākuma, bet 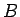 - beigu
punkts). Sadala šo līkni ar punktiem
- beigu
punkts). Sadala šo līkni ar punktiem
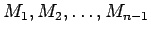 (5.6. zīm.). Savienojot blakus esošos punktus ar
taisnes nogriežņiem, iegūst līknē
(5.6. zīm.). Savienojot blakus esošos punktus ar
taisnes nogriežņiem, iegūst līknē 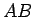 ievilktu lauztu līniju, kas
sastāv no nogriežņiem
ievilktu lauztu līniju, kas
sastāv no nogriežņiem
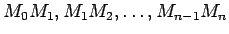 , kur
, kur
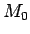 sakrīt ar punktu
sakrīt ar punktu 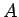 , bet
, bet 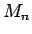 sakrīt ar punktu
sakrīt ar punktu 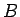 .
.
Aprēķina šīs ievilktās lauztās līnijas perimetru
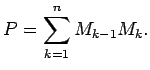 |
(5.3) |
Apzīmē ar
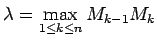 .
.
-
5.1. definīcija.
- Ja summai (5.3) eksistē galīga robeža
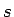 , kad
, kad
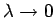 , t.i., jebkuram
, t.i., jebkuram
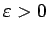 eksistē tāds
eksistē tāds 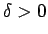 , ka visiem līknes
, ka visiem līknes
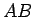 sasmalcinājumiem ar soli
sasmalcinājumiem ar soli
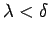 izpildās nevienādība
izpildās nevienādība
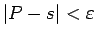 , tad līkni
, tad līkni 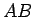 sauc par rektificējamu
(iztaisnojamu), pie tam robežu
sauc par rektificējamu
(iztaisnojamu), pie tam robežu 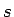 sauc par līknes garumu.
sauc par līknes garumu.
Tādējādi



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 5.3. Līknes garuma aprēķināšana ar noteikto
Augstāk: 5. NOTEIKTĀ INTEGRĀĻA LIETOJUMI
Iepriekšējais: 5.1. Laukuma aprēķināšana ar noteikto integrāli
2002-11-06
![]() (
(![]() - līknes sākuma, bet
- līknes sākuma, bet ![]() - beigu
punkts). Sadala šo līkni ar punktiem
- beigu
punkts). Sadala šo līkni ar punktiem
![]() (5.6. zīm.). Savienojot blakus esošos punktus ar
taisnes nogriežņiem, iegūst līknē
(5.6. zīm.). Savienojot blakus esošos punktus ar
taisnes nogriežņiem, iegūst līknē ![]() ievilktu lauztu līniju, kas
sastāv no nogriežņiem
ievilktu lauztu līniju, kas
sastāv no nogriežņiem
![]() , kur
, kur
![]() sakrīt ar punktu
sakrīt ar punktu ![]() , bet
, bet ![]() sakrīt ar punktu
sakrīt ar punktu ![]() .
.
![]() .
.