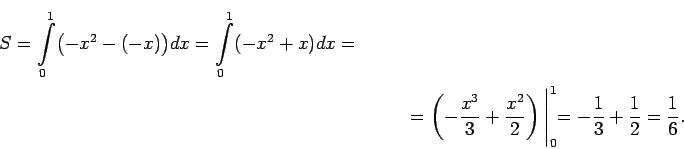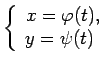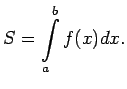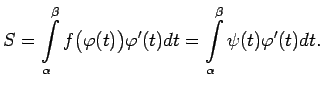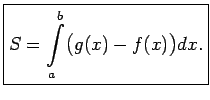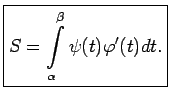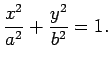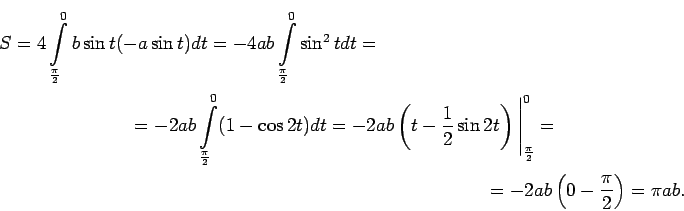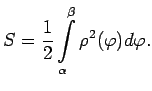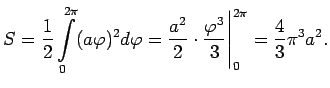Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 5.2. Rektificējama (iztaisnojama) līkne un tās
Augstāk: 5. NOTEIKTĀ INTEGRĀĻA LIETOJUMI
Iepriekšējais: 5. NOTEIKTĀ INTEGRĀĻA LIETOJUMI
Laukumu izskaitļošana ir viens no pamatuzdevumiem, kas noveda pie
noteiktā integrāļa jēdziena.
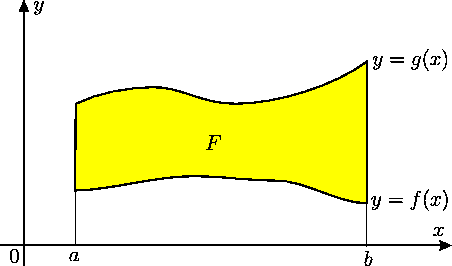
- Apskata plaknes figūru
 , kuru no augšas ierobežo intervālā
, kuru no augšas ierobežo intervālā
![$ [a;b]$](img524.gif) nepārtrauktas funkcijas
nepārtrauktas funkcijas 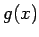 grafiks, no apakšas - šajā
intervālā nepārtrauktas funkcijas
grafiks, no apakšas - šajā
intervālā nepārtrauktas funkcijas 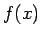 grafiks, pie tam visiem
grafiks, pie tam visiem
![$ x\in[a;b]$](img664.gif)
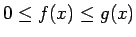 , bet no sāniem - taisnes
, bet no sāniem - taisnes 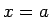 un
un
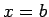 (5.1. zīm.).
(5.1. zīm.).
Figūra  - kvadrējama kā divu kvadrējamu figūru (līklīnijas trapeču
- kvadrējama kā divu kvadrējamu figūru (līklīnijas trapeču
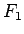 un
un 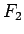 ) starpība, pie tam
) starpība, pie tam
Tādējādi
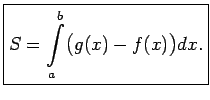 |
(5.1) |
- Apskata plaknes figūru
 , kuru no augšas ierobežo intervālā
, kuru no augšas ierobežo intervālā
![$ [a;b]$](img524.gif) nepārtrauktas funkcijas
nepārtrauktas funkcijas 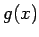 grafiks, no apakšas - šajā
intervālā nepārtrauktas funkcijas
grafiks, no apakšas - šajā
intervālā nepārtrauktas funkcijas 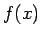 grafiks, pie tam visiem
grafiks, pie tam visiem
![$ x\in[a;b]$](img664.gif)
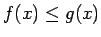 , bet no sāniem - taisnes
, bet no sāniem - taisnes 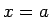 un
un 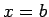 (5.2. zīm.).
(5.2. zīm.).
Atšķirībā no 1. gadījuma šoreiz funkcijas 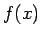 un
un 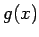 intervālā
intervālā
![$ [a;b]$](img524.gif) var pieņemt arī negatīvas vērtības.
var pieņemt arī negatīvas vērtības.
Apzīmē ar
![$ -A=\inf\limits_{[a;b]}f(x)=\min\limits_{[a;b]}f(x)$](img1034.gif)
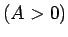 .
.
Apskata plaknes figūru 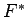 , kuru no apakšas ierobežo funkcijas
, kuru no apakšas ierobežo funkcijas
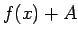 grafiks, no augšas - funkcijas
grafiks, no augšas - funkcijas 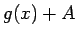 grafiks, bet no
sāniem - taisnes
grafiks, bet no
sāniem - taisnes 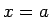 un
un 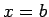 (5.2. zīm.).
(5.2. zīm.).
Figūras 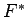 un
un  ir vienādas, tāpēc
ir vienādas, tāpēc 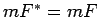 . Figūras
. Figūras 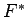 laukumu var izskaitļot pēc formulas (5.1), jo funkcijas
laukumu var izskaitļot pēc formulas (5.1), jo funkcijas
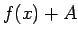 ,
, 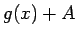 intervālā
intervālā ![$ [a;b]$](img524.gif) ir nenegatīvas.
tādējādi
ir nenegatīvas.
tādējādi
-
5.1. piezīme.
-

- Formula (5.1) ir spēkā arī tajos gadījumos, kad
visa figūra
 vai arī šīs figūras daļa atrodas zem abscisu ass.
vai arī šīs figūras daļa atrodas zem abscisu ass.
- Bieži doto plaknes figūru
 vajag sadalīt galīga skaita
tādās figūrās, kuru laukumus var aprēķināt pēc formulas
(5.1). Dotās figūras laukums būs vienāds ar tās daļu
laukumu summu.
vajag sadalīt galīga skaita
tādās figūrās, kuru laukumus var aprēķināt pēc formulas
(5.1). Dotās figūras laukums būs vienāds ar tās daļu
laukumu summu.
-
5.1. piemērs.
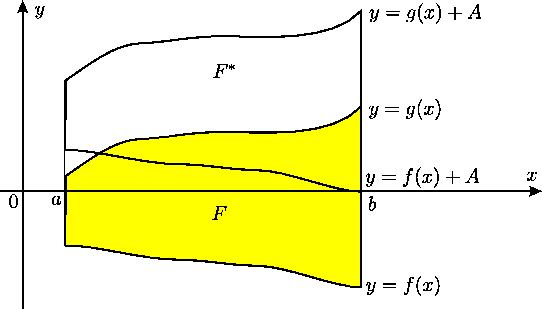
- Aprēķināt laukumu figūrai, kuru ierobežo parabola
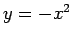 un taisne
un taisne 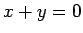 .
.
Koordinātu sistēmā konstruē parabolu 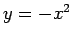 un taisni
un taisni 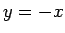 ,
iegūst plaknes figūru
,
iegūst plaknes figūru  (5.3. zīm.).
Figūru no augšas ierobežo parabola
(5.3. zīm.).
Figūru no augšas ierobežo parabola 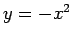 , bet no apakšas - taisne
, bet no apakšas - taisne
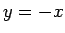 .
.
- Apskata līklīnijas trapeci, kuru no augšas ierobežo
parametriskā veidā uzdota līkne ar vienādojumiem
pie tam
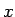 maiņai no
maiņai no 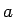 līdz
līdz 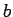
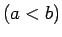 atbilst
atbilst 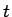 maiņa no
maiņa no
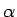 līdz
līdz 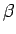 .
.
Funkcija
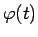 - stingri monotona un nepārtraukti
diferencējama, bet
- stingri monotona un nepārtraukti
diferencējama, bet 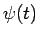 - nepārtraukta atbilstošajā intervālā.
Kā zināms, minētā sistēma parametriskā veidā uzdod intervālā
- nepārtraukta atbilstošajā intervālā.
Kā zināms, minētā sistēma parametriskā veidā uzdod intervālā
![$ [a;b]$](img524.gif) nepārtrauktu funkciju
nepārtrauktu funkciju 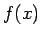 .
.
Līklīnijas trapeces laukumu var aprēķināt pēc formulas
(5.1):
Formulā (5.1) izpilda mainīgā aizvietošanu
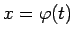 un iegūst:
Tādējādi
un iegūst:
Tādējādi
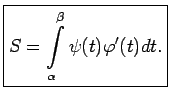 |
(5.2) |
-
5.2. piemērs.
- Aprēķināt laukumu figūrai, kuru ierobežo elipse
Elipses parametriskais vienādojums ir
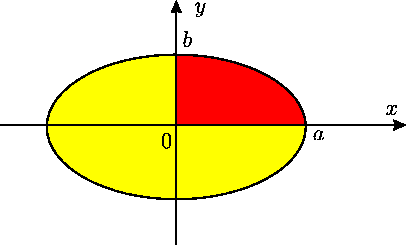
Pēc formulas (5.2) izskaitļo figūras tās daļas, kas
atrodas 1. kvadrantā, laukumu (5.4. zīm.).
Argumenta 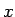 maiņai no 0 līdz
maiņai no 0 līdz 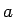 atbilst parametra
atbilst parametra 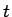 maiņa no
maiņa no
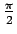 līdz 0.
līdz 0.
-
5.3. piemērs.
- Aprēķināt laukumu figūrai, kuru ierobežo Arhimeda
spirāles
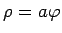
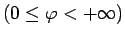 viena vītne un
polārā ass.
viena vītne un
polārā ass.
Lai aprakstītu Arhimeda spirāles vienu vītni, parametrs 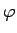 mainās no 0 līdz
mainās no 0 līdz 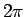 (5.5. zīm.).
(5.5. zīm.).
Laukuma aprēķināšanai lieto līklīnijas sektora laukuma aprēķināšanas
formulu



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 5.2. Rektificējama (iztaisnojama) līkne un tās
Augstāk: 5. NOTEIKTĀ INTEGRĀĻA LIETOJUMI
Iepriekšējais: 5. NOTEIKTĀ INTEGRĀĻA LIETOJUMI
2002-11-06
![]() - kvadrējama kā divu kvadrējamu figūru (līklīnijas trapeču
- kvadrējama kā divu kvadrējamu figūru (līklīnijas trapeču
![]() un
un ![]() ) starpība, pie tam
) starpība, pie tam
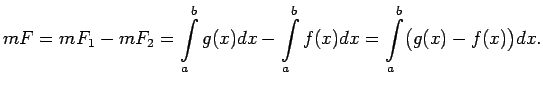
![]() un
un ![]() intervālā
intervālā
![]() var pieņemt arī negatīvas vērtības.
var pieņemt arī negatīvas vērtības.
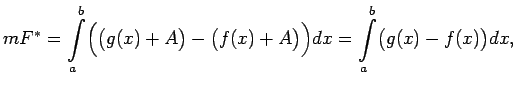
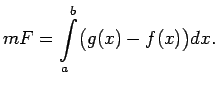

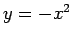 un taisne
un taisne 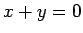 .
.