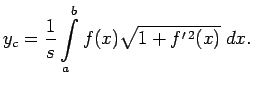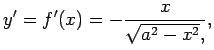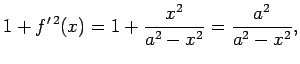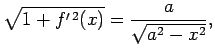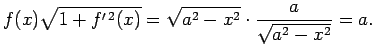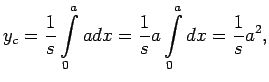Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 5.6. Homogēnas plaknes figūras statisko momentu
Augstāk: 5. NOTEIKTĀ INTEGRĀĻA LIETOJUMI
Iepriekšējais: 5.4. Ķermeņa tilpuma aprēķināšana ar noteikto
-
5.2. definīcija.
- Par materiālu līniju sauc ģeometrisku līniju,
kuras jebkuram lokam ir noteikta masa.
Apskata materiālu līniju  , kas no ģeometriskā viedokļa ir
intervālā
, kas no ģeometriskā viedokļa ir
intervālā ![$ [a;b]$](img524.gif) nepārtraukti diferencējamas funkcijas
nepārtraukti diferencējamas funkcijas 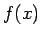 grafiks (5.14. zīm.). Materiālās līnijas lineāro
blīvumu raksturo intervālā
grafiks (5.14. zīm.). Materiālās līnijas lineāro
blīvumu raksturo intervālā ![$ [a;b]$](img524.gif) nepārtraukta funkcija
nepārtraukta funkcija 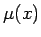 .
.
Izveido loka  sasmalcinājumu ar punktu
sasmalcinājumu ar punktu
palīdzību (tiek iegūts arī intervāla ![$ [a;b]$](img524.gif) sasmalcinājums
sasmalcinājums
Katru no elementārlokiem
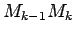 aizstāj ar atbilstošu taisnes
nogriezni, kura garums (tika aprēķināts jau iepriekš) ir
aizstāj ar atbilstošu taisnes
nogriezni, kura garums (tika aprēķināts jau iepriekš) ir
kur
![$ \xi_k\in[x_{k-1},x_k]$](img1083.gif) .
.
Pieņem, ka katrā loka elementārdaļā lineārais blīvums ir konstants un
vienāds ar
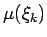 .
.
Elementārloka
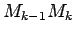 masa aptuveni ir vienāda ar
bet visas līknes
masa aptuveni ir vienāda ar
bet visas līknes 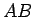 masa aptuveni ir vienāda ar
masa aptuveni ir vienāda ar
Par līknes 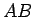 masu nosauc šīs summas robežu. Šāda summa ir
intervālā
masu nosauc šīs summas robežu. Šāda summa ir
intervālā ![$ [a;b]$](img524.gif) nepārtrauktas funkcijas
nepārtrauktas funkcijas
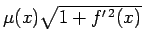 integrālsumma, tāpēc
eksistē galīga robeža no šīs summas, kad sasmalcinājuma solis
tiecas uz nulli, pie tam šī robeža ir vienāda ar noteikto
integrāli
integrālsumma, tāpēc
eksistē galīga robeža no šīs summas, kad sasmalcinājuma solis
tiecas uz nulli, pie tam šī robeža ir vienāda ar noteikto
integrāli
Tādējādi
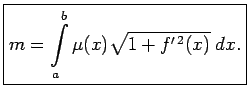 |
(5.9) |
-
5.4. piezīme.
- Ja materiālā līnija ir homogēna, tad lineārais blīvums
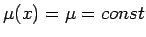 un
un
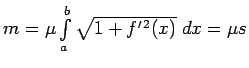 , kur
, kur 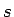 ir līnijas
ir līnijas 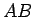 garums.
garums.
-
5.3. definīcija.
- Par materiāla punkta5.2 statisko momentu
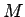 pret kādu asi sauc šī punkta
masas
pret kādu asi sauc šī punkta
masas 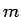 reizinājumu ar punkta attālumu
reizinājumu ar punkta attālumu 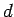 līdz asij, kas ņemts
ar plusa zīmi, ja materiālais punkts atrodas vienā pusē no ass, un
ar mīnusa zīmi, - ja tas atrodas otrā pusē no ass. Tādējādi ar
precizitāti līdz zīmei
līdz asij, kas ņemts
ar plusa zīmi, ja materiālais punkts atrodas vienā pusē no ass, un
ar mīnusa zīmi, - ja tas atrodas otrā pusē no ass. Tādējādi ar
precizitāti līdz zīmei
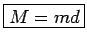 .
.
-
5.4. definīcija.
- Par materiālo punktu sistēmas statisko momentu pret
asi sauc atsevišķo sistēmas punktu statisko momentu summu.
Koordinātu sistēmā apskata materiālu punktu sistēmu
Šo punktu masas apzīmē atbilstoši ar
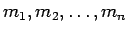 . Šo
materiālo punktu sistēmas statiskie momenti pret koordinātu asīm
ir
. Šo
materiālo punktu sistēmas statiskie momenti pret koordinātu asīm
ir
Apskata materiālas līknes loku 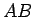 un sadala to elementārdaļās
(5.16. zīm.).
un sadala to elementārdaļās
(5.16. zīm.).
Elementārloka
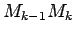 masa aptuveni ir vienāda ar
kur
masa aptuveni ir vienāda ar
kur
![$ \xi_k\in[x_{k-1},x_k]$](img1083.gif) .
.
Uzskata, ka šī elementārloka masa ir koncentrēta punktā
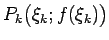 . Šādu materiālo punktu sistēmas
statiskie momenti pret koordinātu asīm atbilstoši ir
un
. Šādu materiālo punktu sistēmas
statiskie momenti pret koordinātu asīm atbilstoši ir
un
Materiālās līknes loka 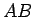 statiskie momenti attiecībā pret
koordinatu asīm ir aptuveni vienādi ar šīm summām. Par līknes loka
statiskie momenti attiecībā pret
koordinatu asīm ir aptuveni vienādi ar šīm summām. Par līknes loka
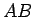 statiskiem momentiem pret koordinātu asīm nosauc šo summu
robežas, t.i.,
statiskiem momentiem pret koordinātu asīm nosauc šo summu
robežas, t.i.,
kur
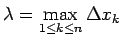 .
.
(Pamatot robežu eksistenci).
Tādējādi
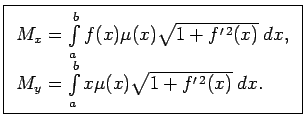 |
(5.10) |
-
5.5. definīcija.
- Par dotās materiālo punktu sistēmas masas
centru
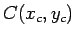 sauc tādu punktu, kurā koncentrējot visas šīs
sistēmas masu
sauc tādu punktu, kurā koncentrējot visas šīs
sistēmas masu 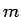 , tā statiskie momenti pret koordinātu asīm ir
vienādi ar sistēmas statiskiem momentiem pret šīm asīm.
, tā statiskie momenti pret koordinātu asīm ir
vienādi ar sistēmas statiskiem momentiem pret šīm asīm.
Tādējādi 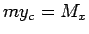 un
un 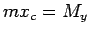 jeb
jeb
Materiālo punktu sistēmai
bet materiālās līknes lokam 
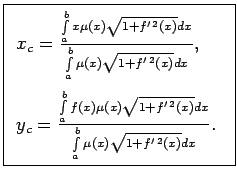 |
(5.11) |
-
5.5. piezīme.
- Ja materiāla līkne ir homogēna (
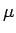 - const), tad
- const), tad
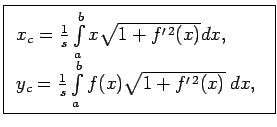 |
(5.12) |
kur
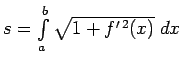 ir līknes
loka
ir līknes
loka  garums.
garums.
-
5.7. piemērs.
- Aprēķināt masas centru homogēnas riņķa līnijas
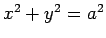 lokam pirmajā kvadrantā.
lokam pirmajā kvadrantā.
Tā kā loks ir simetrisks attiecībā pret koordinātu sistēmas pirmā
kvadranta bisektrisi, tad masas centrs
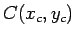 atrodas uz
šīs bisektrises, tāpēc
atrodas uz
šīs bisektrises, tāpēc 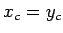 .
.
Pēc formulas (5.12)
Atrod
Tāpēc
kur
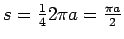 .
.
Tādējādi



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 5.6. Homogēnas plaknes figūras statisko momentu
Augstāk: 5. NOTEIKTĀ INTEGRĀĻA LIETOJUMI
Iepriekšējais: 5.4. Ķermeņa tilpuma aprēķināšana ar noteikto
2002-11-06
![]() , kas no ģeometriskā viedokļa ir
intervālā
, kas no ģeometriskā viedokļa ir
intervālā ![]() nepārtraukti diferencējamas funkcijas
nepārtraukti diferencējamas funkcijas ![]() grafiks (5.14. zīm.). Materiālās līnijas lineāro
blīvumu raksturo intervālā
grafiks (5.14. zīm.). Materiālās līnijas lineāro
blīvumu raksturo intervālā ![]() nepārtraukta funkcija
nepārtraukta funkcija ![]() .
.
![]() sasmalcinājumu ar punktu
sasmalcinājumu ar punktu
![]() aizstāj ar atbilstošu taisnes
nogriezni, kura garums (tika aprēķināts jau iepriekš) ir
aizstāj ar atbilstošu taisnes
nogriezni, kura garums (tika aprēķināts jau iepriekš) ir
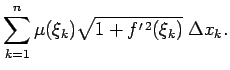
![]() masu nosauc šīs summas robežu. Šāda summa ir
intervālā
masu nosauc šīs summas robežu. Šāda summa ir
intervālā ![]() nepārtrauktas funkcijas
nepārtrauktas funkcijas
![]() integrālsumma, tāpēc
eksistē galīga robeža no šīs summas, kad sasmalcinājuma solis
tiecas uz nulli, pie tam šī robeža ir vienāda ar noteikto
integrāli
integrālsumma, tāpēc
eksistē galīga robeža no šīs summas, kad sasmalcinājuma solis
tiecas uz nulli, pie tam šī robeža ir vienāda ar noteikto
integrāli
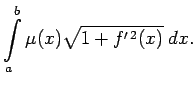
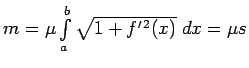 , kur
, kur 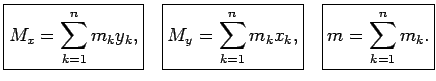
![]() un sadala to elementārdaļās
(5.16. zīm.).
un sadala to elementārdaļās
(5.16. zīm.).
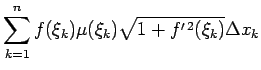
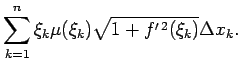
![]() statiskie momenti attiecībā pret
koordinatu asīm ir aptuveni vienādi ar šīm summām. Par līknes loka
statiskie momenti attiecībā pret
koordinatu asīm ir aptuveni vienādi ar šīm summām. Par līknes loka
![]() statiskiem momentiem pret koordinātu asīm nosauc šo summu
robežas, t.i.,
statiskiem momentiem pret koordinātu asīm nosauc šo summu
robežas, t.i.,
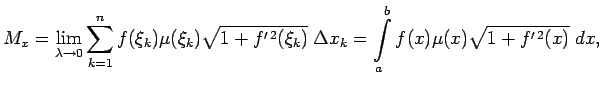
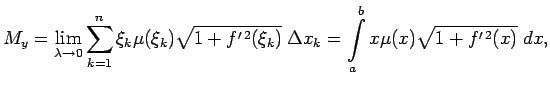
![]() un
un ![]() jeb
jeb
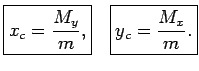
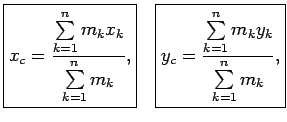
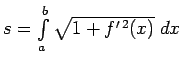 ir līknes
loka
ir līknes
loka ![]() atrodas uz
šīs bisektrises, tāpēc
atrodas uz
šīs bisektrises, tāpēc ![]() .
.