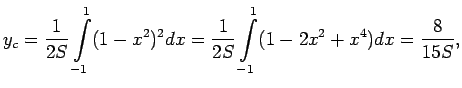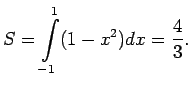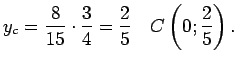Matemātika DU TSC
Nākamais: 5.7. Jautājumi Augstāk: 5. NOTEIKTĀ INTEGRĀĻA LIETOJUMI Iepriekšējais: 5.5. Materiālas līnijas masas, statisko momentu

5.6. Homogēnas plaknes figūras statisko momentu un masas centra aprēķināšana ar noteikto integrāli

Apskata līklīnijas trapeci kā materiālu figūru ar konstantu blīvumu $\mu$, kas izsaka laukuma vienas vienības masu.

Izveido intervāla $[a;b]$ sasmalcinājumu

$$a=x_0<x_1<\cdots<x_{k-1}<x_k<\cdots<x_n=b$$

ar sasmalcinājuma soli $\lambda=\max\limits_{1\leq k\leq n}\Delta x_k$.

Līklīnijas trapece tiek sadalīta elementārjoslās (5.18. zīm.).

5.18. zīm.

Izvēlas patvaļīgu $\xi_k\in[x_{k-1};x_k]$ $(k=1,2,\ldots,n)$. Katras elementārjoslas laukums aptuveni vienāds ar $f(\xi_k)\Delta x_k$, bet masa ir $\mu f(\xi_k)\Delta x_k$. Uzskata, ka elementārjoslas masa ir koncentrēta punktā $P_k\left(\xi_k;\frac{1}{2}f(\xi_k)\right)$. Šādas punktu sistēmas statiskie momenti pret koordinātu asīm atbilstoši ir

$$\sum\limits_{k=1}^n\frac{1}{2}f(\xi_k)\mu f(\xi_k)\Delta x_k= \frac{1}{2}\mu\sum\limits_{k=1}^nf^2(\xi_k)\Delta x_k,$$

$$\sum\limits_{k=1}^n\xi_k\mu f(\xi_k)\Delta x_k= \mu\sum\limits_{k=1}^n\xi_kf(\xi_k)\Delta x_k.$$

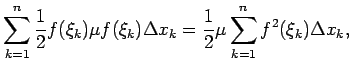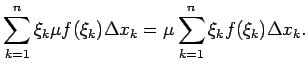Šīs summas aptuveni izsaka līklīnijas trapeces statiskos momentus pret koordinātu asīm.

Līklīnijas trapeces statiskie momenti pret koordinātu asīm ir vienādi

$$M_x=\lim\limits_{\lambda\rightarrow 0}\frac{1}{2}\mu\sum\limits_{... ...0}\sum\limits_{k=1}^nf^2(\xi_k)\Delta x_k=\frac{1}{2}\mu\int\limits_a^bf^2(x)dx$$

un

$$M_y=\lim\limits_{\lambda\rightarrow 0}\mu\sum\limits_{k=1}^n\xi_kf(\xi_k)\Delta x_k= \mu\int\limits_a^bxf(x)dx\/.$$

(Pamatot šādu robežu eksistenci.)

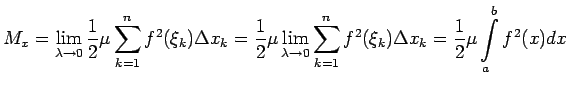
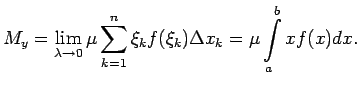
Tādējādi

$$\boxed{ \begin{array}{l} M_x=\frac{1}{2}\mu\int\limits_a^bf^2(x)dx, \\ M_y=\mu\int\limits_a^bxf(x)dx. \\ \end{array}}$$ (5.13)

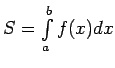Līklīnijas trapeces masa $m=\mu S$, kur $S=\int\limits_a^bf(x)dx$ - līklīnijas trapeces laukums.

Masas centra koordinātas

$$\boxed{\begin{array}{l} x_c=\frac{M_y}{m}=\frac{1}{S}\int\limits_... ...dx, \\ y_c=\frac{M_x}{m}=\frac{1}{2S}\int\limits_a^bf^2(x)dx. \\ \end{array}}$$ (5.14)

5.8. piemērs. 

Aprēķināt masas centru homogēnai figūrai, kuru ierobežo parabola $y=1-x^2$ un abscisu (5.19. zīm.).

5.19. zīm.

Tā kā figūra ir simetriska attiecībā pret ordinātu asi, tad $x_c=0$.

Atrod

$$y_c=\frac{1}{2S}\int\limits_{-1}^1(1-x^2)^2dx= \frac{1}{2S}\int\limits_{-1}^1(1-2x^2+x^4)dx=\frac{8}{15S}\/,$$

kur

$$S=\int\limits_{-1}^1(1-x^2)dx=\frac{4}{3}\/.$$

Tādējādi

$$y_c=\frac{8}{15}\cdot\frac{3}{4}=\frac{2}{5}\quad C\left(0;\frac{2}{5}\right)\/.$$

5.6. piezīme. 

Ja homogēnu plaknes figūru no augšas ierobežo līnija
$y=g(x)$, no apakšas $y=f(x)$, bet no sāniem taisnes $x=a$ un $x=b$ (5.20. zīm.), tad figūras masas centra koordinātas atrod pēc formulām

$$\boxed{\begin{array}{l} x_c=\frac{1}{S}\int\limits_a^bx\bigl(g(x)... ...\ y_c=\frac{1}{2S}\int\limits_a^bx\bigl(g^2(x)-f^2(x)\bigr)dx.\\ \end{array}}$$ (5.15)

5.20. zīm.

Matemātika DU TSC
Nākamais: 5.7. Jautājumi Augstāk: 5. NOTEIKTĀ INTEGRĀĻA LIETOJUMI Iepriekšējais: 5.5. Materiālas līnijas masas, statisko momentu