


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.3. Funkciju integrējamības nepieciešamais un pietiekamais
Augstāk: 2. NOTEIKTAIS INTEGRĀLIS
Iepriekšējais: 2.1. Noteiktā integrāļa jēdziens
Apskata intervālā ![$ [a;b]$](img524.gif) ierobežotu funkciju
ierobežotu funkciju  . Sasmalcina šo
intervālu ar soli
. Sasmalcina šo
intervālu ar soli 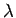 . Tā kā funkcija ir ierobežota
intervālā
. Tā kā funkcija ir ierobežota
intervālā ![$ [a;b]$](img524.gif) , tad tā būs ierobežota katrā no intervāliem
, tad tā būs ierobežota katrā no intervāliem
![$ [x_{k-1};x_k]$](img526.gif) .
.
Eksistē galīgi
![$ m_k=\inf\limits_{[x_{k-1}; x_k]}f(x)$](img527.gif) un
un
![$ M_k=\sup\limits_{[x_{k-1}; x_k]}f(x)$](img528.gif)
 .
.
Izveido šādas summas:
un
-
2.3. definīcija.
- Par apakšējo (vai augšējo) Darbū2.1 summu sauc
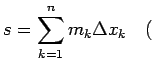
vai
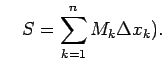
-
2.4. piezīme.
- Atšķirībā no integrālsummas, kas atkarīga gan no
intervāla
![$ [a;b]$](img524.gif) sasmalcinājuma, gan no starppunktu izvēles, Darbū
summas ir atkarīgas tikai no intervāla sasmalcinājuma.
sasmalcinājuma, gan no starppunktu izvēles, Darbū
summas ir atkarīgas tikai no intervāla sasmalcinājuma.
- 1. īpašība.
- Intervāla
![$ [a;b]$](img524.gif) jebkuram sasmalcinājumam
izpildās nevienādība
jebkuram sasmalcinājumam
izpildās nevienādība
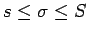 .
.
(Pierādīt patstāvīgi).
- 2. īpašība.
- Intervāla
![$ [a;b]$](img524.gif) jebkuram fiksētam
sasmalcinājumam un jebkuram
jebkuram fiksētam
sasmalcinājumam un jebkuram
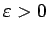 starppunktus
starppunktus 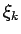 var izvēlēties tā, lai izpildās nevienādība
var izvēlēties tā, lai izpildās nevienādība
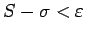 (analogi
(analogi
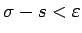 ).
).
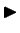 Tā kā
Tā kā
![$ M_k=\sup\limits_{[x_{k-1}; x_k]}f(x)$](img528.gif) ,
tad saskaņā ar funkcijas augšējā sliekšņa definīciju eksistē tāds
,
tad saskaņā ar funkcijas augšējā sliekšņa definīciju eksistē tāds
![$ \xi_k\in[x_{k-1};x_k]$](img536.gif) , ka izpildās nevienādība
, ka izpildās nevienādība
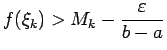
jeb
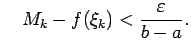
Nevienādības abas puses
reizina ar
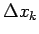 :
Sasummē visas šādas nevienādības un iegūst, ka
:
Sasummē visas šādas nevienādības un iegūst, ka
Analogi var parādīt, ka starppunktus var izvēlēties tā, lai izpildās
nevienādība
- 3. īpašība.
- Ja intervāla
![$ [a;b]$](img524.gif) sasmalcinājumam pievieno
jaunus dalījuma punktus, tad augšējā Darbū summa nevar
palielināties, bet apakšējā Darbū summa nevar samazināties.
sasmalcinājumam pievieno
jaunus dalījuma punktus, tad augšējā Darbū summa nevar
palielināties, bet apakšējā Darbū summa nevar samazināties.
 Intervāla
Intervāla ![$ [a;b]$](img524.gif) sasmalcinājumam
sasmalcinājumam
pievieno vienu dalījuma punktu
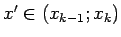 (
(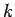 -
fiksēts).
-
fiksēts).
Apzīmē ar
Acīmredzami,
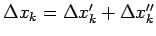 ,
,
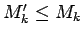 ,
,
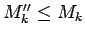 .
.
Apskata sākotnējā sasmalcinājuma un iegūtā sasmalcinājuma augšējo
Darbū summu starpību
Tātad 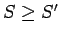 .
.
Analogi pierāda, ka 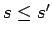 .
.
- 4. īpašība.
- Intervāla
![$ [a;b]$](img524.gif) jebkuriem diviem
sasmalcinājumiem viena sasmalcinājuma apakšējā Darbū summa
nepārsniedz otra sasmalcinājuma augšējo Darbū summu, t.i.,
jebkuriem diviem
sasmalcinājumiem viena sasmalcinājuma apakšējā Darbū summa
nepārsniedz otra sasmalcinājuma augšējo Darbū summu, t.i.,
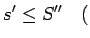
analogi
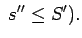
(Pierādīt patstāvīgi).
- 5. īpašība.
- Apakšējo Darbū summu kopai
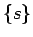 eksistē galīgs
augšējais slieksnis
eksistē galīgs
augšējais slieksnis
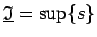 , bet augšējo Darbū
summu kopai
, bet augšējo Darbū
summu kopai 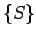 eksistē galīgs apakšējais slieksnis
eksistē galīgs apakšējais slieksnis
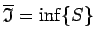 .
.
(Pierādīt patstāvīgi).
- 6. īpašība.
- Intervālā
![$ [a;b]$](img524.gif) jebkuram sasmalcinājumam
izpildās nevienādība
jebkuram sasmalcinājumam
izpildās nevienādība
 Tā kā
Tā kā
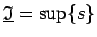 ,
tad
,
tad
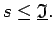 |
(2.1) |
Analogi
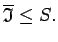 |
(2.2) |
Atliek pierādīt, ka
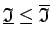 .
.
Pieņem pretējo, t.i., ka
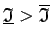 . Izvēlas
. Izvēlas
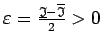 .
Tā kā
.
Tā kā
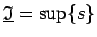 , tad eksistē tāda Darbū
apakšējā summa
, tad eksistē tāda Darbū
apakšējā summa 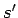 , ka
, ka
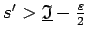 . Analogi
eksistē tāda
. Analogi
eksistē tāda 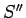 , ka
, ka
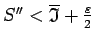 .
.
Apskata
Tātad 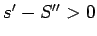 . Šī nevienādība ir pretrunā ar Darbū summu
4. īpašību. Tādējādi
. Šī nevienādība ir pretrunā ar Darbū summu
4. īpašību. Tādējādi
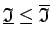 . Apvienojot
šo nevienādību ar nevienādībām (2.1) un
(2.2) iegūst, ka
. Apvienojot
šo nevienādību ar nevienādībām (2.1) un
(2.2) iegūst, ka
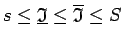 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.3. Funkciju integrējamības nepieciešamais un pietiekamais
Augstāk: 2. NOTEIKTAIS INTEGRĀLIS
Iepriekšējais: 2.1. Noteiktā integrāļa jēdziens
2002-11-06
![]() ierobežotu funkciju
ierobežotu funkciju ![]() . Sasmalcina šo
intervālu ar soli
. Sasmalcina šo
intervālu ar soli ![]() . Tā kā funkcija ir ierobežota
intervālā
. Tā kā funkcija ir ierobežota
intervālā ![]() , tad tā būs ierobežota katrā no intervāliem
, tad tā būs ierobežota katrā no intervāliem
![]() .
.
![$ M_k=\sup\limits_{[x_{k-1}; x_k]}f(x)$](img528.gif)
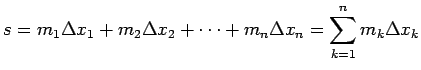
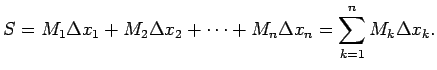
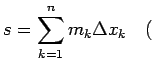 vai
vai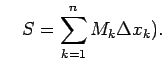
![]() Tā kā
Tā kā
![$ M_k=\sup\limits_{[x_{k-1}; x_k]}f(x)$](img528.gif) ,
tad saskaņā ar funkcijas augšējā sliekšņa definīciju eksistē tāds
,
tad saskaņā ar funkcijas augšējā sliekšņa definīciju eksistē tāds
![]() , ka izpildās nevienādība
, ka izpildās nevienādība
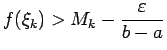 jeb
jeb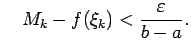
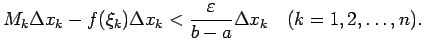
![]() Intervāla
Intervāla ![]() sasmalcinājumam
sasmalcinājumam
![$\displaystyle M_k=\sup\limits_{[x_{k-1};x_k]}f(x),\quad
M'_k=\sup\limits_{[x_{k-1};x']}f(x),\quad
M''_k=\sup\limits_{[x';x_k]}f(x),$](img545.gif)
![]() ,
,
![]() ,
,
![]() .
.
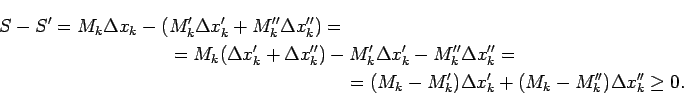
![]() .
.
![]() Tā kā
Tā kā
![]() ,
tad
,
tad
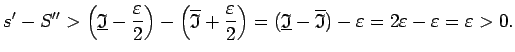
![]() . Šī nevienādība ir pretrunā ar Darbū summu
4. īpašību. Tādējādi
. Šī nevienādība ir pretrunā ar Darbū summu
4. īpašību. Tādējādi
![]() . Apvienojot
šo nevienādību ar nevienādībām (2.1) un
(2.2) iegūst, ka
. Apvienojot
šo nevienādību ar nevienādībām (2.1) un
(2.2) iegūst, ka
![]() .
.
![]()