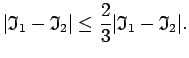Apskata intervālā
Apskata intervālā ![]() definētu funkciju
definētu funkciju ![]() . Sasmalcina šo
intervālu ar starppunktu palīdzību:
. Sasmalcina šo
intervālu ar starppunktu palīdzību:
Katrā no intervāliem
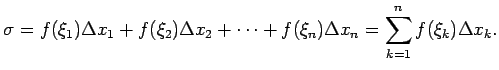
Šādu summu ![]() sauc par funkcijas
sauc par funkcijas ![]() integrālsummu
intervālā
integrālsummu
intervālā ![]() , kas atbilst konkrētam intervāla sasmalcinājumam
un konkrētai starppunktu
, kas atbilst konkrētam intervāla sasmalcinājumam
un konkrētai starppunktu ![]() izvēlei (turpmāk:
integrālsumma).
izvēlei (turpmāk:
integrālsumma).
Robežu
![]() sauc par funkcijas
sauc par funkcijas
![]() noteikto integrāli
intervālā
noteikto integrāli
intervālā
![]() un apzīmē ar simbolu
un apzīmē ar simbolu
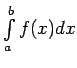 .
.
Tādējādi noteiktā integrāļa definēšanas formula ir:
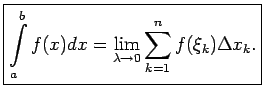
Šajā formulā
![]() sauc par integrēšanas
mainīgo,
sauc par integrēšanas
mainīgo,
![]() - par zemintegrāļa
funkciju,
- par zemintegrāļa
funkciju,
![]() - par zemintegrāļa
izteiksmi,
- par zemintegrāļa
izteiksmi,
![]() - par integrēšanas apakšējo
robežu,
- par integrēšanas apakšējo
robežu,
![]() - par integrēšanas augšējo
robežu,
- par integrēšanas augšējo
robežu,
![]() - par integrēšanas
intervālu.
- par integrēšanas
intervālu.
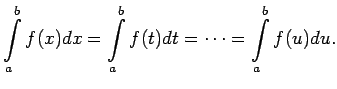
Apskata intervālā ![]() konstantu funkciju
konstantu funkciju ![]() . Šādai
funkcijai
. Šādai
funkcijai
![]() neatkarīgi no starppunktu
neatkarīgi no starppunktu ![]() izvēles.
Integrālsumma
izvēles.
Integrālsumma
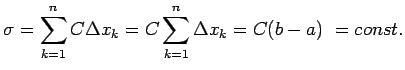
Acīmredzami, eksistē galīga robeža
![]() .
Seko, ka
.
Seko, ka ![]() ir integrējama funkcija intervālā
ir integrējama funkcija intervālā ![]() un
un
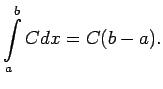
Tādējādi funkcijas ierobežotība intervālā ![]() ir tās
integrējamības šajā intervālā
nepieciešamais nosacījums.
ir tās
integrējamības šajā intervālā
nepieciešamais nosacījums.
Piemēram, Dirihlē funkcija
![$\displaystyle f(x)=\left\{\begin{array}{ccc}
0, & \text{ja} & x~-\text{intervāl...
... \text{ja} & x~-\text{intervāla $[a,b]$ racionāls skaitlis,}
\end{array}\right.$](img502.gif)
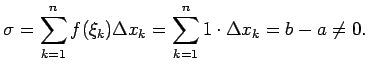
Ja par starppunktiem ![]() izvēlas iracionālus skaitļus, tad
izvēlas iracionālus skaitļus, tad
![]() . Acīmredzami, robeža no
. Acīmredzami, robeža no ![]() , kad
, kad
![]() , neeksistē un Dirihlē funkcija nav integrējama
funkcija.
, neeksistē un Dirihlē funkcija nav integrējama
funkcija.
Ja funkcijai ![]() intervālā
intervālā ![]() eksistē noteiktais integrālis,
tad vienīgā veidā.
eksistē noteiktais integrālis,
tad vienīgā veidā.
![]() Pieņem pretējo, t.i., ka funkcijas
Pieņem pretējo, t.i., ka funkcijas ![]() integrālsummai intervālā
integrālsummai intervālā ![]() eksistē divas dažādas
galīgas robežas
eksistē divas dažādas
galīgas robežas
![]() . Izvēlas
. Izvēlas
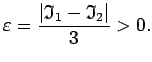
Tā kā
![]() ir integrālsummas robeža, tad šādam
ir integrālsummas robeža, tad šādam
![]() eksistē
eksistē
![]() , ka visiem
, ka visiem
![]() izpildās nevienādība
izpildās nevienādība
Analogi - priekš
![]() : eksistē
: eksistē
![]() , ka
visiem
, ka
visiem
![]() izpildās nevienādība
izpildās nevienādība
Apzīmē ar
![]() un sasmalcinājumam
ar soli
un sasmalcinājumam
ar soli
![]() atbilstošo integrālsummu
apzīmē
ar
atbilstošo integrālsummu
apzīmē
ar ![]() . Intervāla
. Intervāla ![]() sasmalcinājumam ar soli
sasmalcinājumam ar soli
![]() izpildās vienlaicīgi nevienādības
izpildās vienlaicīgi nevienādības
Apskata
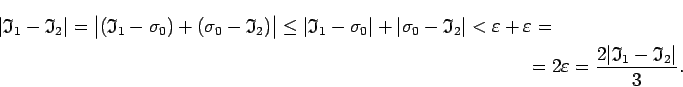
Tātad