


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.4. Integrējamu funkciju klases
Augstāk: 2. NOTEIKTAIS INTEGRĀLIS
Iepriekšējais: 2.2. Darbū summas un to īpašības
-
2.2. teorēma.
- Intervālā
![$ [a;b]$](img524.gif) definēta un ierobežota funkcija
ir integrējama šajā intervālā tad un tikai tad, ja jebkuram
definēta un ierobežota funkcija
ir integrējama šajā intervālā tad un tikai tad, ja jebkuram
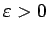 eksistē tāds
eksistē tāds 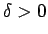 , ka visiem
, ka visiem
![$ [a;b]$](img524.gif) sasmalcinājumiem ar soli
sasmalcinājumiem ar soli
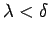 izpildās
nevienādība
izpildās
nevienādība
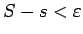 .
.
 Nepieciešamība. Tā kā funkcija
Nepieciešamība. Tā kā funkcija  -
integrējama intervālā
-
integrējama intervālā ![$ [a;b]$](img524.gif) , tad eksistē galīga robeža
, tad eksistē galīga robeža
Pamatojoties uz šādas robežas definīciju, jebkuram
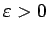 eksistē tāds
eksistē tāds 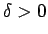 , ka visiem
, ka visiem ![$ [a;b]$](img524.gif) sasmalcinājumiem ar
soli
sasmalcinājumiem ar
soli
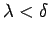 izpildās nevienādība
izpildās nevienādība
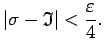 |
(2.3) |
Fiksē vienu tādu intervāla ![$ [a;b]$](img524.gif) sasmalcinājumu, kuram izpildās
nevienādība (2.3). Šim intervāla
sasmalcinājumu, kuram izpildās
nevienādība (2.3). Šim intervāla ![$ [a;b]$](img524.gif) sasmalcinājumam atbilstošās Darbū summas apzīmē ar
sasmalcinājumam atbilstošās Darbū summas apzīmē ar 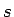 un
un 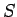 . Pēc
Darbū summu 2. īpašības starppunktus var
izvēlēties tā, lai izpildās nevienādības
. Pēc
Darbū summu 2. īpašības starppunktus var
izvēlēties tā, lai izpildās nevienādības
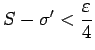 |
(2.4) |
un
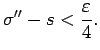 |
(2.5) |
Nevienādība (2.3) izpildās arī integrālsummām
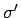 un
un 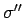 .
.
Apskata
Tādējādi
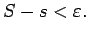 |
(2.6) |
Pietiekamība. Pēc dotā jebkuram
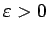 eksistē tāds
eksistē tāds
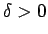 , ka visiem intervāla
, ka visiem intervāla ![$ [a;b]$](img524.gif) sasmalcinājumiem ar soli
sasmalcinājumiem ar soli
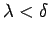 izpildās nevienādība (2.6).
izpildās nevienādība (2.6).
Pēc Darbū summu 6. īpašības
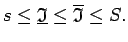 |
(2.7) |
Apskata
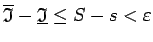 .
.
Tātad nenegatīvā konstante
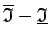 ir pēc patikas
maza. Seko, ka šī konstante ir nulle jeb
ir pēc patikas
maza. Seko, ka šī konstante ir nulle jeb
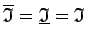 .
Tāpēc nevienādība (2.7) izskatās šādi:
.
Tāpēc nevienādība (2.7) izskatās šādi:
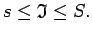 |
(2.8) |
Pēc Darbū summu 1. īpašības
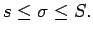 |
(2.9) |
No nevienādības (2.8) atņemot nevienādību
(2.9), iegūst nevienādību
jeb
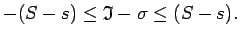 |
(2.10) |
Nevienādība (2.10) ir ekvivalenta nevienādībai
Tā kā
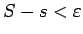 , tad
, tad
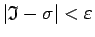 .
Seko, ka
.
Seko, ka
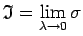 .
Tātad funkcija
.
Tātad funkcija  ir integrējama intervālā
ir integrējama intervālā ![$ [a;b]$](img524.gif) .
.
-
2.5. piezīme.
- No 2.2. teorēmas izriet, ka vienādība
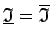 ir funkcijas integrējamības
intervālā
ir funkcijas integrējamības
intervālā ![$ [a;b]$](img524.gif) nepieciešamais un pietiekamais nosacījums.
nepieciešamais un pietiekamais nosacījums.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.4. Integrējamu funkciju klases
Augstāk: 2. NOTEIKTAIS INTEGRĀLIS
Iepriekšējais: 2.2. Darbū summas un to īpašības
2002-11-06
![]() Nepieciešamība. Tā kā funkcija
Nepieciešamība. Tā kā funkcija ![]() -
integrējama intervālā
-
integrējama intervālā ![]() , tad eksistē galīga robeža
, tad eksistē galīga robeža
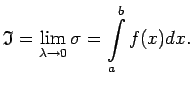
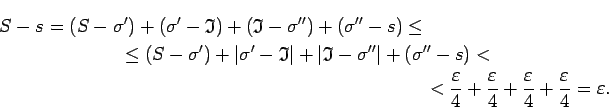
![]() eksistē tāds
eksistē tāds
![]() , ka visiem intervāla
, ka visiem intervāla ![]() sasmalcinājumiem ar soli
sasmalcinājumiem ar soli
![]() izpildās nevienādība (2.6).
izpildās nevienādība (2.6).
![]() .
.
![]() ir pēc patikas
maza. Seko, ka šī konstante ir nulle jeb
ir pēc patikas
maza. Seko, ka šī konstante ir nulle jeb
![]() .
Tāpēc nevienādība (2.7) izskatās šādi:
.
Tāpēc nevienādība (2.7) izskatās šādi:
![]() , tad
, tad
![]() .
Seko, ka
.
Seko, ka
![]() .
Tātad funkcija
.
Tātad funkcija ![]() ir integrējama intervālā
ir integrējama intervālā ![]() .
.
![]()