Ja funkcija ![]() ir nepārtraukta slēgtā intervālā
ir nepārtraukta slēgtā intervālā ![]() , tad tā ir
integrējama šajā intervālā.
, tad tā ir
integrējama šajā intervālā.
Ja funkcija ![]() ir nepārtraukta slēgtā intervālā
ir nepārtraukta slēgtā intervālā ![]() , tad tā ir
integrējama šajā intervālā.
, tad tā ir
integrējama šajā intervālā.
![]() Tā kā funkcija
Tā kā funkcija ![]() ir nepārtraukta slēgtā
intervālā
ir nepārtraukta slēgtā
intervālā ![]() , tad, pirmkārt, tā ir ierobežota šajā intervālā
un, otrkārt, saskaņā ar Kantora teorēmu tā ir vienmērīgi
nepārtraukta šajā intervālā. Saskaņā ar intervālā vienmērīgi
nepārtrauktas funkcijas definīciju jebkuram
, tad, pirmkārt, tā ir ierobežota šajā intervālā
un, otrkārt, saskaņā ar Kantora teorēmu tā ir vienmērīgi
nepārtraukta šajā intervālā. Saskaņā ar intervālā vienmērīgi
nepārtrauktas funkcijas definīciju jebkuram
![]() eksistē tāds
eksistē tāds ![]() , ka visiem
, ka visiem
![]() , kuriem
, kuriem
![]() , izpildās nevienādība
, izpildās nevienādība
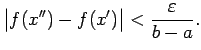
Ja izveido intervāla ![]() sasmalcinājumu ar soli
sasmalcinājumu ar soli
![]() ,
tad visiem
,
tad visiem
![]() izpildās
nevienādība
izpildās
nevienādība
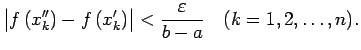
Saskaņā ar Veierštrāsa otro teorēmu tā sasniedz katrā no šiem intervāliem savu vismazāko un vislielāko vērtību. Tas nozīmē, ka intervāla
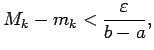
![$\displaystyle m_k=\inf\limits_{[x_{k-1};x_k]}f(x)=\min\limits_{[x_{k-1};x_k]}f(x),\;\;\;
M_k=\sup\limits_{[x_{k-1};x_k]}f(x)=\max\limits_{[x_{k-1};x_k]}f(x)\/,$](img601.gif)
Apskata
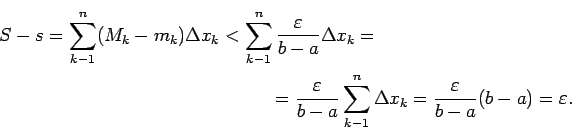
Ja funkcija ![]() ir ierobežota un monotona intervālā
ir ierobežota un monotona intervālā ![]() ,
tad tā ir integrējama šajā intervālā.
,
tad tā ir integrējama šajā intervālā.
![]() Noteiktības dēļ pieņemsim, ka
Noteiktības dēļ pieņemsim, ka ![]() ir
intervālā
ir
intervālā ![]() nedilstoša funkcija.
nedilstoša funkcija.
Šoreiz
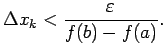
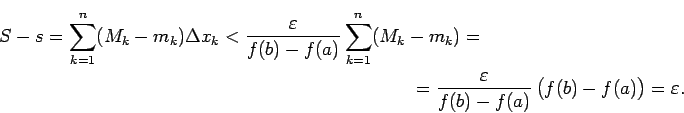
Saskaņa ar 2.2. teorēmu ![]() ir intervālā
ir intervālā ![]() integrējama funkcija.
integrējama funkcija.
![]()