Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.6. Noteiktā integrāļa vispārinājums
Augstāk: 2. NOTEIKTAIS INTEGRĀLIS
Iepriekšējais: 2.4. Integrējamu funkciju klases
- Lemma.
- Ja funkcija
 ir definēta kopā
ir definēta kopā 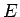 un
visiem
un
visiem
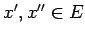 izpildās nevienādība
(
izpildās nevienādība
(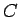 - konstante), tad arī
- konstante), tad arī 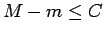 , kur
, kur
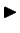 Noteiktības dēļ pieņemsim, ka
Noteiktības dēļ pieņemsim, ka
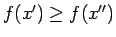 . Saskaņā ar doto visiem
. Saskaņā ar doto visiem
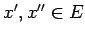 izpildās nevienādība
izpildās nevienādība
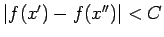 . Seko, ka
. Seko, ka
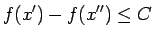
jeb
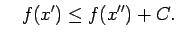
Fiksētam 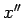 šī nevienādība norāda, ka eksistē galīgs
šī nevienādība norāda, ka eksistē galīgs

jeb

No šīs nevienādības seko, ka visiem 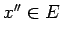 izpildās
izpildās
 . Analogi eksistē galīgs
. Analogi eksistē galīgs
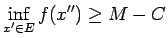
jeb
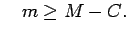
Tādējādi
- 1. īpašība.
- Ja
 ir integrējama
funkcija intervālā
ir integrējama
funkcija intervālā ![$ [a;b]$](img524.gif) , tad arī
, tad arī 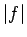 ir integrējama
funkcija šajā intervālā.
ir integrējama
funkcija šajā intervālā.
 Apskata intervāla
Apskata intervāla ![$ [a;b]$](img524.gif) patvaļīgu
sasmalcinājumu. Šim sasmalcinājumam un funkcijai
patvaļīgu
sasmalcinājumu. Šim sasmalcinājumam un funkcijai  atbilstošās Darbū summas apzīmē ar
atbilstošās Darbū summas apzīmē ar  un
un 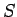 . Ar
. Ar 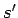 un
un  apzīmē funkcijai
apzīmē funkcijai 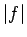 atbilstošās Darbū summas (sasmalcinājums
iepriekšējais). Saskaņā ar moduļa īpašību visiem
atbilstošās Darbū summas (sasmalcinājums
iepriekšējais). Saskaņā ar moduļa īpašību visiem
![$ x', x''\in
[x_{k-1};x_k]$](img626.gif) izpildās nevienādība
izpildās nevienādība
Tā kā
kur
![$ m_k=\inf\limits_{[x_{k-1}; x_k]}f(x)$](img527.gif) ,
,
![$ M_k=\sup\limits_{[x_{k-1}; x_k]}f(x)$](img528.gif) , tad
, tad
Saskaņā ar lemmu (šoreiz funkcija ir 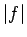 , bet
, bet  )
)
kur
![$ M_k'=\sup\limits_{[x_{k-1};x_k]}\bigl\vert f(x)\bigr\vert$](img632.gif) ,
,
![$ m_k'=\inf\limits_{[x_{k-1};x_k]}\bigl\vert f(x)\bigr\vert$](img633.gif) . Tāpēc
. Tāpēc
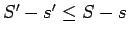 .
.
Tā kā funkcija  ir integrējama intervālā
ir integrējama intervālā ![$ [a,b]$](img476.gif) , tad pielietojot
2.2. teorēmu, viegli saskatīt, ka šajā intervālā ir
integrējama arī funkcija
, tad pielietojot
2.2. teorēmu, viegli saskatīt, ka šajā intervālā ir
integrējama arī funkcija 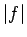 .
.

-
2.6. piezīme.
- 1. īpašībai apgrieztais
apgalvojums nav spēkā.
Piemēram, funkcija
nav integrējama intervālā ![$ [a;b]$](img524.gif) .2.2 Šīs funkcijas modulis
.2.2 Šīs funkcijas modulis 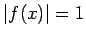 ir integrējama
funkcija (kā konstante) šajā intervālā.
ir integrējama
funkcija (kā konstante) šajā intervālā.
- 2. īpašība.
- Ja
 ir integrējama
funkcija intervālā
ir integrējama
funkcija intervālā ![$ [a;b]$](img524.gif) , tad tā ir integrējama arī intervālā
, tad tā ir integrējama arī intervālā
![$ [c;d]\subset [a;b]$](img637.gif) .
.
(Pierādīt patstāvīgi).2.3
- 3. īpašība.
- Ja
 un
un 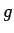 ir
integrējamas funkcijas intervālā
ir
integrējamas funkcijas intervālā ![$ [a;b]$](img524.gif) , tad arī
, tad arī
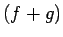 ir
integrējama funkcija šajā intervālā, pie tam
ir
integrējama funkcija šajā intervālā, pie tam
 Tā kā
Tā kā  ir integrējama funkcija intervālā
ir integrējama funkcija intervālā
![$ [a;b]$](img524.gif) , tad jebkuram
, tad jebkuram
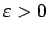 eksistē tāds
eksistē tāds
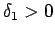 ,
ka intervāla
,
ka intervāla ![$ [a;b]$](img524.gif) visiem sasmalcinājumiem ar soli
visiem sasmalcinājumiem ar soli
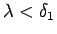 izpildās nevienādība
izpildās nevienādība
Analogi - iepriekš izvēlētajam
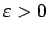 eksistē tāds
eksistē tāds
 , ka intervāla
, ka intervāla ![$ [a;b]$](img524.gif) visiem sasmalcinājumiem ar
soli
visiem sasmalcinājumiem ar
soli
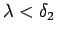 izpildās nevienādība
izpildās nevienādība
Apskata
Nevienādība
norāda, ka
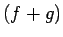 ir integrējama funkcija intervālā
ir integrējama funkcija intervālā ![$ [a;b]$](img524.gif) , pie tam
jeb
, pie tam
jeb
-
2.7. piezīme.
- Ar matemātiskās indukcijas metodi šo īpašību var
vispārināt uz jebkuru galīga skaita integrējamu funkciju summu.
- 4. īpašība.
- Ja
 ir integrējama
funkcija intervālā
ir integrējama
funkcija intervālā ![$ [a;b]$](img524.gif) un
un 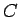 ir patvaļīga konstante, tad
ir patvaļīga konstante, tad 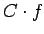 ir integrējama funkcija šajā intervālā, pie tam
ir integrējama funkcija šajā intervālā, pie tam
 Apskatīsim divus iespējamos gadījumus.
Apskatīsim divus iespējamos gadījumus.
- Ja
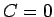 , tad
, tad 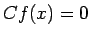 un
un 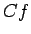 ir integrējama funkcija (kā
konstante). Vienādība acīmredzami izpildās.
ir integrējama funkcija (kā
konstante). Vienādība acīmredzami izpildās.
- Pieņemsim, ka
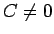 . Tā kā
. Tā kā  ir integrējama funkcija intervālā
ir integrējama funkcija intervālā
![$ [a;b]$](img524.gif) , tad jebkuram
, tad jebkuram
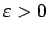 eksistē
tāds
eksistē
tāds 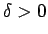 , ka intervāla
, ka intervāla ![$ [a;b]$](img524.gif) visiem sasmalcinājumiem ar
soli
visiem sasmalcinājumiem ar
soli
 izpildās nevienādība
kur
izpildās nevienādība
kur
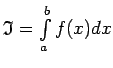 .
.
Apskata
Nevienādība
norāda, ka  ir integrējama funkcija intervālā
ir integrējama funkcija intervālā ![$ [a;b]$](img524.gif) , pie
tam
, pie
tam
-
2.8. piezīme.
- No 3. un
4. īpašības izriet noteiktā integrāļa linearitātes
īpašība, t.i., ja
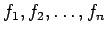 ir intervālā
ir intervālā ![$ [a;b]$](img524.gif) integrējamas funkcijas un
integrējamas funkcijas un
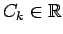 (
(
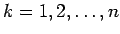 ), tad arī
), tad arī
 ir
integrējama funkcija šajā intervālā, pie tam
ir
integrējama funkcija šajā intervālā, pie tam
- 5. īpašība.
- Ja
 ir integrējama
funkcija intervālā
ir integrējama
funkcija intervālā ![$ [a;b]$](img524.gif) un visiem
un visiem ![$ x\in[a;b]$](img664.gif) izpildās
nevienādība
izpildās
nevienādība
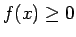 , tad arī
, tad arī
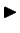 Pieņem pretējo, t.i., ka
Pieņem pretējo, t.i., ka
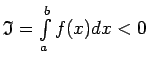 . Saskaņā ar noteiktā
integrāļa definīciju jebkuram
. Saskaņā ar noteiktā
integrāļa definīciju jebkuram
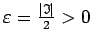 eksistē tāds
eksistē tāds 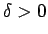 ,
ka intervāla
,
ka intervāla ![$ [a;b]$](img524.gif) visiem sasmalcinājumiem ar soli
visiem sasmalcinājumiem ar soli
 izpildās nevienādība
izpildās nevienādība
Ja
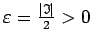 , tad gan
, tad gan
 , gan
, gan
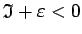 (
(
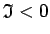 ).
).
Tā kā visi
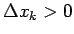 , tad integrālsummā
, tad integrālsummā
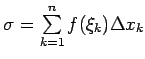 ne visi locekļi ir
nenegatīvi, t.i., ne visi
ne visi locekļi ir
nenegatīvi, t.i., ne visi 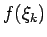 ir nenegatīvi. Rodas pretruna
ar doto, ka visiem
ir nenegatīvi. Rodas pretruna
ar doto, ka visiem ![$ x\in[a;b]$](img664.gif)
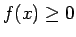 .
.

- 6. īpašība.
- [Noteiktā integrāļa monotonitātes
īpašība]
Ja  ir integrējamas funkcijas intervālā
ir integrējamas funkcijas intervālā ![$ [a;b]$](img524.gif) un visiem
un visiem
![$ x\in[a;b]$](img664.gif) izpildās nevienādība
izpildās nevienādība
 , tad arī
, tad arī
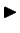 Apskata funkciju
Apskata funkciju
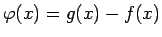 .
Funkcija
.
Funkcija  ir integrējama kā divu integrējamu funkciju
starpība un saskaņā ar 5. īpašību
ir integrējama kā divu integrējamu funkciju
starpība un saskaņā ar 5. īpašību
jo visiem ![$ x\in[a;b]$](img664.gif)
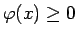 .
.
Saskaņā ar noteiktā integrāļa linearitātes īpašību
Seko, ka
jeb
- 7. īpašība.
- [Noteiktā integrāļa
novērtējums]
Ja  ir integrējama funkcija intervālā
ir integrējama funkcija intervālā ![$ [a;b]$](img524.gif) un visiem
un visiem
![$ x\in[a;b]$](img664.gif) izpildās nevienādība
izpildās nevienādība
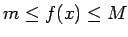
 , tad
, tad
(Pierādīt patstāvīgi2.4).
-
2.9. piezīme.
- Nenegatīvas un nepārtrauktas funkcijas gadījumā
7. īpašībai var sniegt šādu ģeometrisku
interpretāciju: līklīnijas trapeces laukums2.5 ir ieslēgts starp divu
šādu taisnstūru laukumiem (2.1. zīm.). Abiem taisnstūriem un
līklīnijas trapecei ir kopīgs pamats. Pirmā taisnstūra augstums ir
![$ m=\min\limits_{[a;b]}f(x)$](img690.gif) , bet otrā taisnstūra augstums ir
, bet otrā taisnstūra augstums ir
![$ M=\max\limits_{[a;b]}f(x)$](img691.gif) .
.
- 8. īpašība.
- Ja
 ir integrējama funkcija
intervālā
ir integrējama funkcija
intervālā ![$ [a;b]$](img524.gif) , tad
, tad
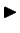 Saskaņā ar 1. īpašību
Saskaņā ar 1. īpašību 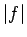 ir integrējama funkcija intervālā
ir integrējama funkcija intervālā ![$ [a;b]$](img524.gif) . Visiem
. Visiem ![$ x\in[a;b]$](img664.gif) izpildās nevienādība
izpildās nevienādība
Saskaņā ar noteiktā integrāļa monotonitātes īpašību
jeb
- 9. īpašība.
- [Noteiktā integrāļa aditivitātes
īpašība]
Ja  ir integrējama funkcija intervālā
ir integrējama funkcija intervālā
![$ [a;b]=[a;c]\cup[c;b]$](img697.gif) , tad
, tad
 ir integrējama katrā no intervāliem
ir integrējama katrā no intervāliem ![$ [a;c]$](img698.gif) ,
, ![$ [c;b]$](img699.gif) un
un
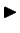 Saskaņā ar 2. īpašību
Saskaņā ar 2. īpašību  ir integrējama funkcija katrā no intervāliem
ir integrējama funkcija katrā no intervāliem ![$ [a;c]$](img698.gif) un
un ![$ [c;b]$](img699.gif) .
Apzīmē ar
.
Apzīmē ar
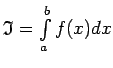 ,
,
 ,
,
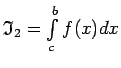 . Atliek pierādīt, ka
. Atliek pierādīt, ka
 .
.
Izveido intervāla ![$ [a;b]$](img524.gif) tādu sasmalcinājumu, lai par vienu tā
sadalījuma punktu būtu
tādu sasmalcinājumu, lai par vienu tā
sadalījuma punktu būtu 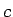 .
.
Šim sasmalcinājumam atbilstošo integrālsummu  sadala summās
sadala summās 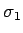 un
un 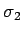 , kur
, kur 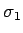 - funkcijas
- funkcijas
 integrālsumma intervālā
integrālsumma intervālā ![$ [a;c]$](img698.gif) , bet
, bet 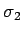 -
funkcijas
-
funkcijas  integrālsumma intervālā
integrālsumma intervālā ![$ [c;b]$](img699.gif) .
Šajā vienādībā pāriet pie robežas, kad sasmalcinājuma solis
.
Šajā vienādībā pāriet pie robežas, kad sasmalcinājuma solis
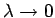 .
.
- 10. īpašība.
- [Teorēma par noteiktā
integrāļa vidējo vērtību]
Ja  - nepārtrauktas funkcijas intervālā
- nepārtrauktas funkcijas intervālā ![$ [a;b]$](img524.gif) , pie tam
funkcija
, pie tam
funkcija 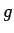 šajā intervālā saglabā zīmi, tad eksistē tāds
šajā intervālā saglabā zīmi, tad eksistē tāds
![$ x_0\in[a;b]$](img708.gif) , ka
, ka
 Abi integrāļi eksistē, jo
Abi integrāļi eksistē, jo 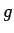 un
un 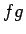 -
nepārtrauktas funkcijas intervālā
-
nepārtrauktas funkcijas intervālā ![$ [a;b]$](img524.gif) (funkcija
(funkcija 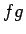 -
nepārtraukta intervālā
-
nepārtraukta intervālā ![$ [a;b]$](img524.gif) kā divu nepārtrauktu funkciju
reizinājums).
kā divu nepārtrauktu funkciju
reizinājums).
Pieņem, ka visiem ![$ x\in[a;b]$](img664.gif)
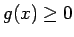 .
.
Apzīmē ar
![$ m=\min\limits_{[a;b]}f(x)$](img690.gif) ,
,
![$ M=\max\limits_{[a;b]}f(x)$](img691.gif) . Saskaņā ar Veierštrāsa otro teorēmu
eksistē tādi
. Saskaņā ar Veierštrāsa otro teorēmu
eksistē tādi
![$ x_1,x_2\in[a;b]$](img712.gif) , ka
, ka 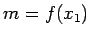 ,
, 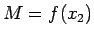 .
.
Visiem ![$ x\in[a;b]$](img664.gif) izpildās nevienādība
izpildās nevienādība
Reizina šo nevienādību ar
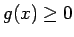
Saskaņā ar noteiktā integrāļa monotonitātes īpašību un
4. īpašību
Tā kā
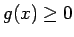 , tad ir iespējami divi gadījumi:
, tad ir iespējami divi gadījumi:
-
 .
.
No nevienādības seko, ka
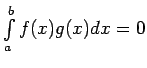 , tāpēc par
, tāpēc par
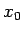 der jebkurš intervāla
der jebkurš intervāla ![$ [a;b]$](img524.gif) punkts.
punkts.
-
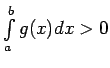 .
.
Izdala nevienādību ar
 .
No šīs nevienādības seko, ka
ir viena no funkcijas
.
No šīs nevienādības seko, ka
ir viena no funkcijas  starpvērtībām. Saskaņā ar
Bolcano-Veierštrāsa teorēmu par nepārtrauktas funkcijas
starpvērtībām eksistē tāds
starpvērtībām. Saskaņā ar
Bolcano-Veierštrāsa teorēmu par nepārtrauktas funkcijas
starpvērtībām eksistē tāds
![$ x_0\in[a;b]$](img708.gif) , ka
jeb
, ka
jeb
- Sekas.
- Ja
 ir nepārtraukta funkcija intervālā
ir nepārtraukta funkcija intervālā ![$ [a;b]$](img524.gif) , tad
eksistē tāds
, tad
eksistē tāds
![$ x_0\in[a;b]$](img708.gif) , ka
, ka
 .
.
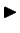 Apskata funkciju
Apskata funkciju 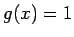 . Saskaņā ar teorēmu
par noteiktā integrāļa vidējo vērtību
. Saskaņā ar teorēmu
par noteiktā integrāļa vidējo vērtību
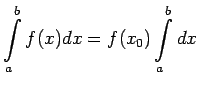
jeb
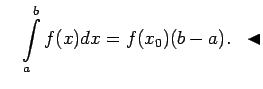
-
2.10. piezīme.
-

- Nenegatīvas un nepārtrauktas funkcijas gadījumā šīm sekām var
sniegt šādu ģeometrisku interpretāciju: eksistē tāds
taisnstūris, kura laukums ir vienāds ar līklīnijas trapeces laukumu
(2.2. zīm.). Taisnstūrim un līklīnijas trapecei ir kopīgs pamats, bet
taisnstūra augstums ir
 .
.
- Nosacījums, lai funkcija
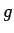 saglabā zīmi, ir būtisks.
Piemēram, ja izvēlas divas intervālā
saglabā zīmi, ir būtisks.
Piemēram, ja izvēlas divas intervālā ![$ [0;2\pi]$](img733.gif) nepārtrauktas
funkcijas
nepārtrauktas
funkcijas
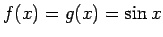 , tad, izskaitļojot
integrāļus2.6
, tad, izskaitļojot
integrāļus2.6
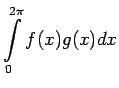
un
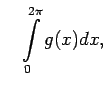
iegūst, ka
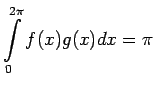
un
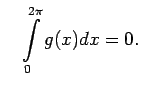
Šajā gadījumā nav tādas vērtības
![$ x_0\in[0;2\pi]$](img739.gif) , kurai izpildītos vienādība
, kurai izpildītos vienādība



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.6. Noteiktā integrāļa vispārinājums
Augstāk: 2. NOTEIKTAIS INTEGRĀLIS
Iepriekšējais: 2.4. Integrējamu funkciju klases
2002-11-06
![]() Noteiktības dēļ pieņemsim, ka
Noteiktības dēļ pieņemsim, ka
![]() . Saskaņā ar doto visiem
. Saskaņā ar doto visiem
![]() izpildās nevienādība
izpildās nevienādība
![]() . Seko, ka
. Seko, ka
![]() šī nevienādība norāda, ka eksistē galīgs
šī nevienādība norāda, ka eksistē galīgs
![]() Apskata intervāla
Apskata intervāla ![]() patvaļīgu
sasmalcinājumu. Šim sasmalcinājumam un funkcijai
patvaļīgu
sasmalcinājumu. Šim sasmalcinājumam un funkcijai ![]() atbilstošās Darbū summas apzīmē ar
atbilstošās Darbū summas apzīmē ar ![]() un
un ![]() . Ar
. Ar ![]() un
un ![]() apzīmē funkcijai
apzīmē funkcijai ![]() atbilstošās Darbū summas (sasmalcinājums
iepriekšējais). Saskaņā ar moduļa īpašību visiem
atbilstošās Darbū summas (sasmalcinājums
iepriekšējais). Saskaņā ar moduļa īpašību visiem
![]() izpildās nevienādība
izpildās nevienādība
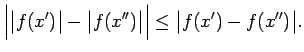
![$ M_k=\sup\limits_{[x_{k-1}; x_k]}f(x)$](img528.gif) , tad
, tad
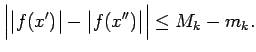
![]() , bet
, bet ![]() )
)
![$ M_k'=\sup\limits_{[x_{k-1};x_k]}\bigl\vert f(x)\bigr\vert$](img632.gif) ,
,
![$\displaystyle f(x)=\left\{\begin{array}{ccl}
1, & \text{ja} & x~-\text{intervāl...
... & x~-\text{intervāla}\; [a;b]\; \text{iracionāls skaitlis,}
\end{array}\right.$](img635.gif)
![]() Tā kā
Tā kā ![]() ir integrējama funkcija intervālā
ir integrējama funkcija intervālā
![]() , tad jebkuram
, tad jebkuram
![]() eksistē tāds
eksistē tāds
![]() ,
ka intervāla
,
ka intervāla ![]() visiem sasmalcinājumiem ar soli
visiem sasmalcinājumiem ar soli
![]() izpildās nevienādība
izpildās nevienādība
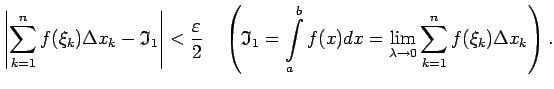
![]() eksistē tāds
eksistē tāds
![]() , ka intervāla
, ka intervāla ![]() visiem sasmalcinājumiem ar
soli
visiem sasmalcinājumiem ar
soli
![]() izpildās nevienādība
izpildās nevienādība
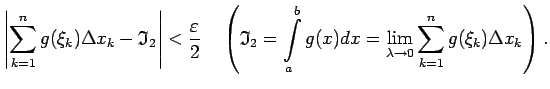
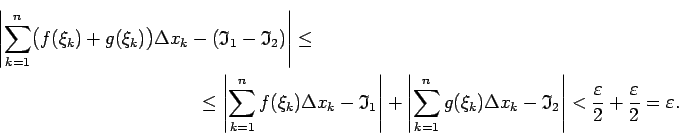
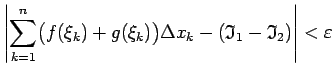
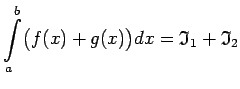
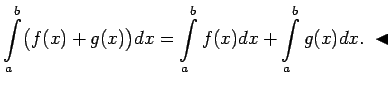

![]() Apskatīsim divus iespējamos gadījumus.
Apskatīsim divus iespējamos gadījumus.
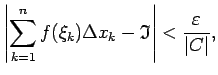
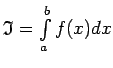 .
.

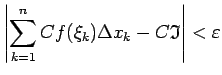
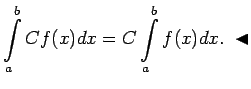
 ir
integrējama funkcija šajā intervālā, pie tam
ir
integrējama funkcija šajā intervālā, pie tam
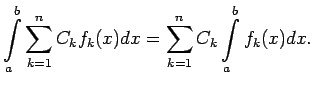

![]() Pieņem pretējo, t.i., ka
Pieņem pretējo, t.i., ka
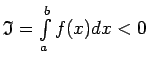 . Saskaņā ar noteiktā
integrāļa definīciju jebkuram
. Saskaņā ar noteiktā
integrāļa definīciju jebkuram
![]() eksistē tāds
eksistē tāds ![]() ,
ka intervāla
,
ka intervāla ![]() visiem sasmalcinājumiem ar soli
visiem sasmalcinājumiem ar soli
![]() izpildās nevienādība
izpildās nevienādība
![]() , tad gan
, tad gan
![]() , gan
, gan
![]() (
(
![]() ).
).
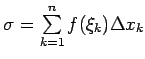 ne visi locekļi ir
nenegatīvi, t.i., ne visi
ne visi locekļi ir
nenegatīvi, t.i., ne visi ![]() ir integrējamas funkcijas intervālā
ir integrējamas funkcijas intervālā ![]() un visiem
un visiem
![]() izpildās nevienādība
izpildās nevienādība
![]() , tad arī
, tad arī
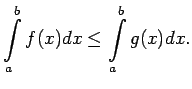
![]() Apskata funkciju
Apskata funkciju
![]() .
Funkcija
.
Funkcija ![]() ir integrējama kā divu integrējamu funkciju
starpība un saskaņā ar 5. īpašību
ir integrējama kā divu integrējamu funkciju
starpība un saskaņā ar 5. īpašību

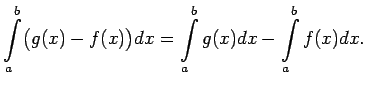
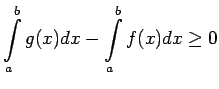
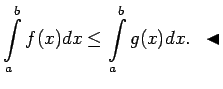
![]() ir integrējama funkcija intervālā
ir integrējama funkcija intervālā ![]() un visiem
un visiem
![]() izpildās nevienādība
izpildās nevienādība
![]()
![]() , tad
, tad

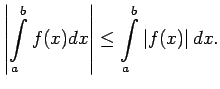
![]() Saskaņā ar 1. īpašību
Saskaņā ar 1. īpašību ![]() ir integrējama funkcija intervālā
ir integrējama funkcija intervālā ![]() . Visiem
. Visiem ![]() izpildās nevienādība
izpildās nevienādība
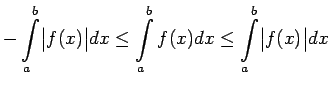
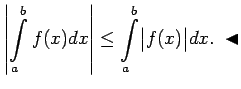
![]() ir integrējama funkcija intervālā
ir integrējama funkcija intervālā
![]() , tad
, tad
![]() ir integrējama katrā no intervāliem
ir integrējama katrā no intervāliem ![]() ,
, ![]() un
un

![]() Saskaņā ar 2. īpašību
Saskaņā ar 2. īpašību ![]() ir integrējama funkcija katrā no intervāliem
ir integrējama funkcija katrā no intervāliem ![]() un
un ![]() .
Apzīmē ar
.
Apzīmē ar
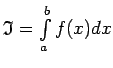 ,
,
 ,
,
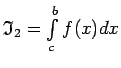 . Atliek pierādīt, ka
. Atliek pierādīt, ka
![]() .
.
![]() - nepārtrauktas funkcijas intervālā
- nepārtrauktas funkcijas intervālā ![]() , pie tam
funkcija
, pie tam
funkcija ![]() šajā intervālā saglabā zīmi, tad eksistē tāds
šajā intervālā saglabā zīmi, tad eksistē tāds
![]() , ka
, ka
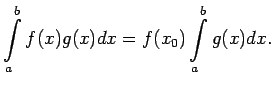
![]() Abi integrāļi eksistē, jo
Abi integrāļi eksistē, jo ![]() un
un ![]() -
nepārtrauktas funkcijas intervālā
-
nepārtrauktas funkcijas intervālā ![]() (funkcija
(funkcija ![]() -
nepārtraukta intervālā
-
nepārtraukta intervālā ![]() kā divu nepārtrauktu funkciju
reizinājums).
kā divu nepārtrauktu funkciju
reizinājums).

![]() , tad ir iespējami divi gadījumi:
, tad ir iespējami divi gadījumi:
 .
.
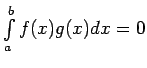 , tāpēc par
, tāpēc par
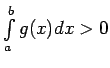 .
.
 .
.
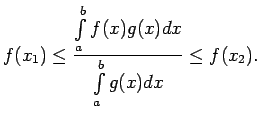
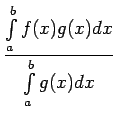
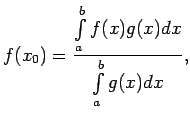
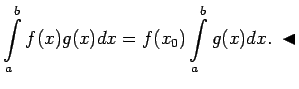
 .
.
![]() Apskata funkciju
Apskata funkciju ![]() . Saskaņā ar teorēmu
par noteiktā integrāļa vidējo vērtību
. Saskaņā ar teorēmu
par noteiktā integrāļa vidējo vērtību
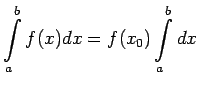 jeb
jeb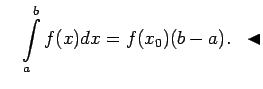
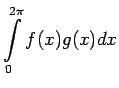 un
un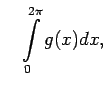
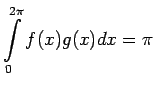 un
un