Definējot noteikto integrāli
 uzskatīja, ka
uzskatīja, ka
Definējot noteikto integrāli
 uzskatīja, ka
uzskatīja, ka
![]() . Taču noteikto integrāli var vispārināt arī attiecībā uz
tādiem gadījumiem, kad
. Taču noteikto integrāli var vispārināt arī attiecībā uz
tādiem gadījumiem, kad ![]() vai
vai ![]() .
.
Uzskata, ka
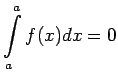 un
un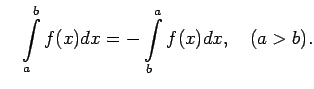
 , uzskata, ka
, uzskata, ka Šādam integrālim
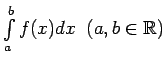 acīmredzami ir spēkā noteiktā integrāļa
1., 2., 3. un 4.
īpašības, bet
5., 6. un 7.
īpašības nav spēkā.
8. īpašības nevienādība iegūst šādu
izskatu
acīmredzami ir spēkā noteiktā integrāļa
1., 2., 3. un 4.
īpašības, bet
5., 6. un 7.
īpašības nav spēkā.
8. īpašības nevienādība iegūst šādu
izskatu
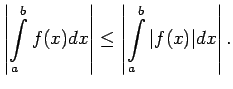
Piemēram, ja ![]() , tad
, tad
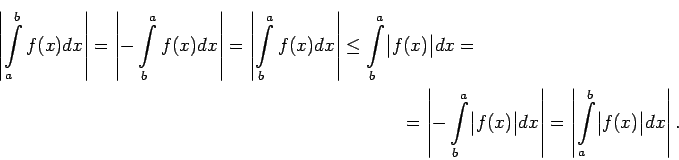
9. īpašība var tikt formulēta šādi:
Ja funkcija
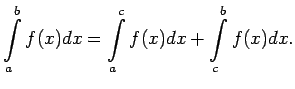
Piemēram, ja ![]() , tad saskaņā ar noteiktā integrāļa aditivitāti
, tad saskaņā ar noteiktā integrāļa aditivitāti
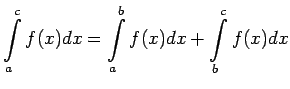
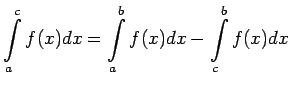
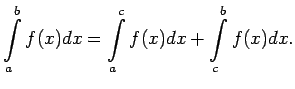
Analogi var pamatot visus pārējos iespējamos gadījumus.
10. īpašība un tās sekas arī ir spēkā.