


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.8. Vingrinājumi
Augstāk: 2.6. Noteiktā integrāļa vispārinājums
Iepriekšējais: 2.6. Noteiktā integrāļa vispārinājums
- Definēt funkcijas
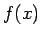 integrālsummu intervālā
integrālsummu intervālā ![$ [a;b]$](img524.gif) .
.
- No kā ir atkarīga integrālsumma, kas sastādīta funkcijai
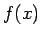 intervālā
intervālā ![$ [a;b]$](img524.gif) ?
?
- Definēt integrālsummas robežu, kad sasmalcinājuma solis
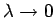 .
.
- Definēt intervālā
![$ [a;b]$](img524.gif) integrējamu funkciju un šīs
funkcijas noteikto integrāli.
integrējamu funkciju un šīs
funkcijas noteikto integrāli.
- Vai noteiktais integrālis ir atkarīgs no tā, ar kādu burtu ir
apzīmēts integrēšanas mainīgais? Atbildi pamatot.
- Kāds ir funkcijas integrējamības nepieciešamais nosacījums?
- Vai katra intervālā
![$ [a;b]$](img524.gif) ierobežota funkcija ir
integrējama šajā intervālā? Atbildi pamatot.
ierobežota funkcija ir
integrējama šajā intervālā? Atbildi pamatot.
- Vai intervālā
![$ [a;b]$](img524.gif) integrējamai funkcijai var eksistēt
divas dažādas noteiktā integrāļa vērtības?
integrējamai funkcijai var eksistēt
divas dažādas noteiktā integrāļa vērtības?
- Definēt funkcijas
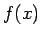 Darbū summas intervālā
Darbū summas intervālā ![$ [a;b]$](img524.gif) .
.
- No kā ir atkarīgas Darbū summas, kas sastādītas funkcijai
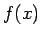 intervālā
intervālā ![$ [a;b]$](img524.gif) ?
?
- Formulēt Darbū summu īpašības.
- Formulēt funkciju integrējamības nepieciešamo un pietiekamo
nosacījumu.
- Formulēt funkciju integrējamības pietiekamos nosacījumus.
- Formulēt īpašību par integrāli no funkcijas moduļa.
- Ir zināms, ka funkcijas modulis ir intervālā
![$ [a;b]$](img524.gif) integrējama funkcija. Vai ir integrējama šajā intervālā pati
funkcija? Atbildi pamatot.
integrējama funkcija. Vai ir integrējama šajā intervālā pati
funkcija? Atbildi pamatot.
- Formulēt noteiktā integrāļa linearitātes īpašību.
- Formulēt īpašību par noteiktā integrāļa zīmi no nenegatīvas
funkcijas.
- Formulēt noteiktā integrāļa monotonitātes īpašību.
- Formulēt īpašību par noteiktā integrāļa novērtējumu.
- Formulēt īpašību par noteiktā integrāļa moduli.
- Formulēt noteiktā integrāļa aditivitātes īpašību.
- Formulēt īpašību par noteiktā integrāļa vidējo vērtību.
- Definēt noteikto integrāli
 , kad
, kad 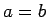 vai
vai 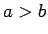 .
.
- Formulēt noteiktā integrāļa
 5., 6., 7. un 8.
īpašību, kad
5., 6., 7. un 8.
īpašību, kad 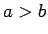 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.8. Vingrinājumi
Augstāk: 2.6. Noteiktā integrāļa vispārinājums
Iepriekšējais: 2.6. Noteiktā integrāļa vispārinājums
2002-11-06
 , kad
, kad  5., 6., 7. un 8.
īpašību, kad
5., 6., 7. un 8.
īpašību, kad  , kad
, kad  5., 6., 7. un 8.
īpašību, kad
5., 6., 7. un 8.
īpašību, kad