


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.2. Plaknes figūras kvadrējamības kritēriji
Augstāk: 4. KVADRĒJAMĪBAS KRITĒRIJI
Iepriekšējais: 4. KVADRĒJAMĪBAS KRITĒRIJI
-
4.1. definīcija.
- Par plaknes figūru
 sauc katru
ierobežotu4.1 plaknes punktu kopu.
sauc katru
ierobežotu4.1 plaknes punktu kopu.
Apskata plaknes figūrā  (4.1. zīm.) visu iespējamo
ievilktu plaknes daudzstūru
(4.1. zīm.) visu iespējamo
ievilktu plaknes daudzstūru 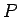
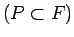 kopu
kopu
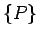 un visu iespējamo apvilktu plaknes daudzstūru
un visu iespējamo apvilktu plaknes daudzstūru
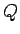
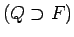 kopu
kopu 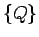 . Plaknes daudzstūra
. Plaknes daudzstūra 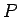 laukumu4.2apzīmē ar
laukumu4.2apzīmē ar 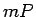 , bet plaknes daudzstūra
, bet plaknes daudzstūra 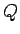 laukumu - atbilstoši
ar
laukumu - atbilstoši
ar 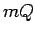 .
.
Skaitļu kopa 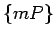 nav tukša4.3 un ir ierobežota no
augšas ar jebkura apvilkta plaknes daudzstūra
nav tukša4.3 un ir ierobežota no
augšas ar jebkura apvilkta plaknes daudzstūra 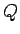 laukumu
laukumu 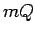 .
.
Eksistē galīgs
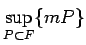 , kuru apzīmē
, kuru apzīmē
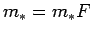 un sauc par plaknes figūras
un sauc par plaknes figūras  iekšējo laukumu.
iekšējo laukumu.
Tādējādi
Plaknes figūras  ārējo laukumu definē
ārējo laukumu definē
(Patstāvīgi pamatot ārējā laukuma eksistenci.)
Tā kā 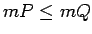 , tad
, tad
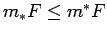 .
.
-
4.2. definīcija.
- Plaknes figūru
 sauc par kvadrējamu, ja
tās iekšējais laukums sakrīt ar ārējo laukumu, t.i.,
sauc par kvadrējamu, ja
tās iekšējais laukums sakrīt ar ārējo laukumu, t.i., 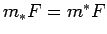 ,
pie tam šo kopīgo skaitli sauc par figūras
,
pie tam šo kopīgo skaitli sauc par figūras  laukumu un apzīmē
laukumu un apzīmē 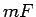 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.2. Plaknes figūras kvadrējamības kritēriji
Augstāk: 4. KVADRĒJAMĪBAS KRITĒRIJI
Iepriekšējais: 4. KVADRĒJAMĪBAS KRITĒRIJI
2002-11-06
![]() (4.1. zīm.) visu iespējamo
ievilktu plaknes daudzstūru
(4.1. zīm.) visu iespējamo
ievilktu plaknes daudzstūru ![]()
![]() kopu
kopu
![]() un visu iespējamo apvilktu plaknes daudzstūru
un visu iespējamo apvilktu plaknes daudzstūru
![]()
![]() kopu
kopu ![]() . Plaknes daudzstūra
. Plaknes daudzstūra ![]() laukumu4.2apzīmē ar
laukumu4.2apzīmē ar ![]() , bet plaknes daudzstūra
, bet plaknes daudzstūra ![]() laukumu - atbilstoši
ar
laukumu - atbilstoši
ar ![]() .
.
![]() ārējo laukumu definē
ārējo laukumu definē
![]() , tad
, tad
![]() .
.