


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.3. Kvadrējamu figūru piemēri
Augstāk: 4. KVADRĒJAMĪBAS KRITĒRIJI
Iepriekšējais: 4.1. Plaknes figūras laukums
-
4.1. teorēma.
- [Kvadrējamības 1. kritērijs]
Plaknes figūra  kvadrējama tad un tikai tad, ja jebkuram
kvadrējama tad un tikai tad, ja jebkuram
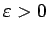 eksistē tāds ievilkts plaknes
daudzstūris
eksistē tāds ievilkts plaknes
daudzstūris 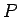 un tāds apvilkts plaknes daudzstūris
un tāds apvilkts plaknes daudzstūris 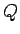
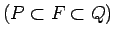 , ka
, ka
 Nepieciešamība.
Nepieciešamība.
Tā kā  - kvadrējama figūra, tad
- kvadrējama figūra, tad 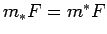 . Saskaņā ar kopas
. Saskaņā ar kopas
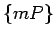 augšējā sliekšņa
augšējā sliekšņa 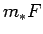 definīciju jebkuram
definīciju jebkuram
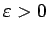 eksistē tāds plaknes daudzstūris
eksistē tāds plaknes daudzstūris 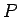
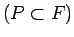 , ka
, ka
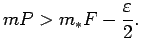 |
(4.1) |
Analogi eksistē tāds 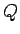
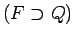 , ka
, ka
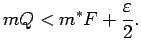 |
(4.2) |
No nevienādības (4.2) atņem (4.1) un iegūst
Pietiekamība.
Šoreiz jebkuram
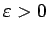 eksistē tādi plaknes daudzstūri
eksistē tādi plaknes daudzstūri 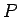 un
un 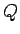
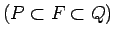 , ka
, ka
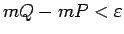 .
.
No  iekšējā laukuma un ārējā laukuma definīcijas seko, ka
Tāpēc
iekšējā laukuma un ārējā laukuma definīcijas seko, ka
Tāpēc
Tā kā
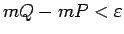 , tad
, tad
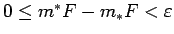 .
Nenegatīvā konstante
.
Nenegatīvā konstante 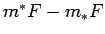 var kļūt pēc patikas maza tikai tad,
kad tā ir nulle.
var kļūt pēc patikas maza tikai tad,
kad tā ir nulle.
Tādējādi 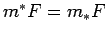 . Plaknes figūra
. Plaknes figūra  - kvadrējama.
- kvadrējama.
-
4.2. teorēma.
- [Kvadrējamības 2. kritērijs]
Plaknes figūra  kvadrējama tad un tikai tad, ja jebkuram
kvadrējama tad un tikai tad, ja jebkuram
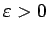 eksistē tāda ievilkta kvadrējama
plaknes figūra
eksistē tāda ievilkta kvadrējama
plaknes figūra 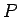 un tāda apvilkta kvadrējama plaknes figūra
un tāda apvilkta kvadrējama plaknes figūra 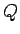
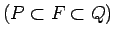 , ka
, ka
 Nepieciešamība.
Nepieciešamība.
Saskaņā ar kvadrējamības 1. kritēriju (skat. 4.1. teorēmu) par tādām
kvadrējamām plaknes figūrām var izvēlēties plaknes daudzstūrus.
Pietiekamība.
Šoreiz jebkuram
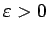 eksistē tādas kvadrējamas plaknes
figūras
eksistē tādas kvadrējamas plaknes
figūras 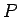 un
un 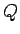
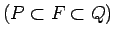 , ka
, ka
Tā kā 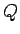 - kvadrējama plaknes figūra, tad eksistē tāds plaknes
daudzstūris
- kvadrējama plaknes figūra, tad eksistē tāds plaknes
daudzstūris
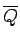
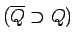 , ka
, ka
Analogi eksistē tāds plaknes daudzstūris
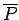
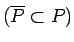 , ka
, ka
Plaknes daudzstūriem
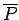 ,
,
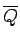
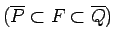 izpildās
izpildās
Plaknes figūra  ir kvadrējama saskaņā ar kvadrējamības
1. kritēriju (skat. 4.1. teorēmu).
ir kvadrējama saskaņā ar kvadrējamības
1. kritēriju (skat. 4.1. teorēmu).



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.3. Kvadrējamu figūru piemēri
Augstāk: 4. KVADRĒJAMĪBAS KRITĒRIJI
Iepriekšējais: 4.1. Plaknes figūras laukums
2002-11-06
![]() Nepieciešamība.
Nepieciešamība.
![]() , tad
, tad
![]() .
Nenegatīvā konstante
.
Nenegatīvā konstante ![]() var kļūt pēc patikas maza tikai tad,
kad tā ir nulle.
var kļūt pēc patikas maza tikai tad,
kad tā ir nulle.
![]() Nepieciešamība.
Nepieciešamība.
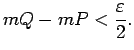
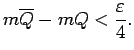
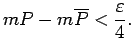
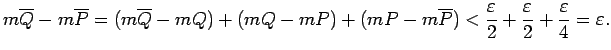
![]() ir kvadrējama saskaņā ar kvadrējamības
1. kritēriju (skat. 4.1. teorēmu).
ir kvadrējama saskaņā ar kvadrējamības
1. kritēriju (skat. 4.1. teorēmu).
![]()