


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3. INTEGRĀLIS AR MAINĪGU AUGŠĒJO ROBEŽU
Augstāk: 2.6. Noteiktā integrāļa vispārinājums
Iepriekšējais: 2.8. Vingrinājumi
- Izmantojot noteiktā integrāļa definīciju,
izskaitļot dotos noteiktos integrāļus:
-
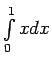 ,
,
-
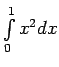 ,
,
-
 .
.
- Piezīme.
- Intervālu
![$ [0;1]$](img776.gif) sadalīt
sadalīt 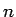 vienādās daļās un par
starppunktiem
vienādās daļās un par
starppunktiem 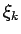 izvēlēties vienu no intervālu
izvēlēties vienu no intervālu
![$ [x_{k-1};x_k]$](img526.gif) galapunktiem, (b) gadījumā izmantot, ka
galapunktiem, (b) gadījumā izmantot, ka
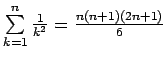 .
.
- Funkcijai
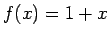 sastādīt Darbū summas un integrālsummu
intervālā
sastādīt Darbū summas un integrālsummu
intervālā ![$ [1;10]$](img779.gif) . Intervālu
. Intervālu ![$ [1;10]$](img779.gif) sadalīt
sadalīt 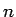 vienādās daļās
un par starppunktiem
vienādās daļās
un par starppunktiem 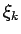 izvēlēties intervālu
izvēlēties intervālu
![$ [x_{k-1};x_k]$](img526.gif) viduspunktus. Atrast robežu no katras Darbū summas un no integrālsummas,
kad
viduspunktus. Atrast robežu no katras Darbū summas un no integrālsummas,
kad
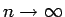 .
.
- Aprēķināt figūras, kuru ierobežo parabola
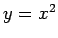 , abscisu
ass un taisne
, abscisu
ass un taisne 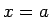
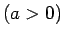 , laukumu.
, laukumu.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3. INTEGRĀLIS AR MAINĪGU AUGŠĒJO ROBEŽU
Augstāk: 2.6. Noteiktā integrāļa vispārinājums
Iepriekšējais: 2.8. Vingrinājumi
2002-11-06
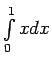 ,
,
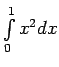 ,
,
 .
.
![$ [0;1]$](img776.gif) sadalīt
sadalīt 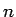 vienādās daļās un par
starppunktiem
vienādās daļās un par
starppunktiem 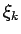 izvēlēties vienu no intervālu
izvēlēties vienu no intervālu
![$ [x_{k-1};x_k]$](img526.gif) galapunktiem, (b) gadījumā izmantot, ka
galapunktiem, (b) gadījumā izmantot, ka
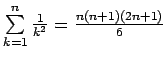 .
.
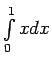 ,
,
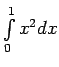 ,
,
 .
.
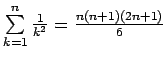 .
.