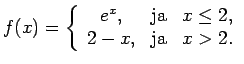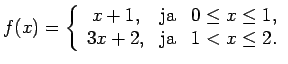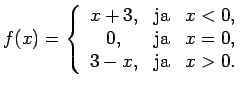Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: LITERATŪRA
Augstāk: 4.8. Slēgtā intervālā nepārtrauktu funkciju pamatīpašības
Iepriekšējais: 4.9. Jautājumi
- Pierādīt funkciju nepārtrauktību:
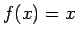 ;
;
-
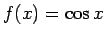 ;
;
-
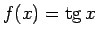 .
.
- Pierādīt 4.1. teorēmu.
- Pierādīt 4.2. teorēmu.
- Pierādīt 4.3. teorēmu.
- Pierādīt 4.4. teorēmu.
- Pierādīt 4.7. teorēmu.
- Pierādīt 4.8. teorēmu.
- Dotajām funkcijām sameklēt pārtraukuma punktus un
noteikt to veidu:
-
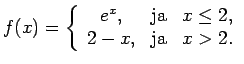
-
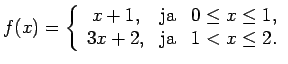
-

-
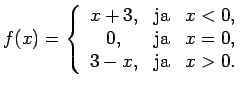
- Pierādīt 4.10. teorēmu dilstošai funkcijai.
- Pierādīt 4.11. teorēmu dilstošai funkcijai.
- Funkcija nepārtraukta intervālā
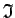 un
punktos
un
punktos
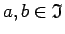 tās vērtības ir ar dažādām zīmēm.
Pierādīt, ka starp
tās vērtības ir ar dažādām zīmēm.
Pierādīt, ka starp  un
un 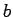 eksistē tāds punkts, kurā
funkcijas vērtība ir nulle.
eksistē tāds punkts, kurā
funkcijas vērtība ir nulle.
- Pierādīt 4.13. teorēmu dilstošai funkcijai.
- Pierādīt funkciju nepārtrauktību:
-
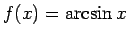 ,
,
-
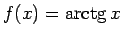 ,
,
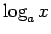 .
.
- Pierādīt, ka katra intervālā nepārtraukta un injektīva
funkcija ir stingri monotona šajā intervālā.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: LITERATŪRA
Augstāk: 4.8. Slēgtā intervālā nepārtrauktu funkciju pamatīpašības
Iepriekšējais: 4.9. Jautājumi
2003-02-24
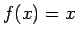 ;
;
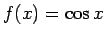 ;
;
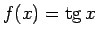 .
.
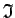 un
punktos
un
punktos
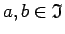 tās vērtības ir ar dažādām zīmēm.
Pierādīt, ka starp
tās vērtības ir ar dažādām zīmēm.
Pierādīt, ka starp  un
un 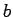 eksistē tāds punkts, kurā
funkcijas vērtība ir nulle.
eksistē tāds punkts, kurā
funkcijas vērtība ir nulle.
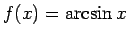 ,
,
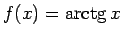 ,
,
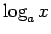 .
.