- ... (skat.1
- Tā bieži apzīmē arī pašu
funkciju
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... periodu2
- Parasti to sauc par
periodu.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... periodiska3
- Skat.[12, 36. lpp.].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... apgabalā4
- Ja
 nav apvēršama
nav apvēršama 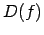 ,
tad izveido funkcijas sašaurinājumu uz kopu, kurā
,
tad izveido funkcijas sašaurinājumu uz kopu, kurā  ir
apvēršama.
ir
apvēršama.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (skat.5
- Tiek izmantota
formula
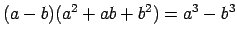 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (skat.6
- Tiek izmantota eksponentfunkcijas
nepārtrauktība.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(skat.7
- Tiek izmantota robeža
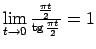 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (skat.8
- Lasa:
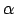 ir omikrons no
ir omikrons no
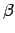 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (skat.9
- Šoreiz
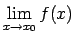 neeksistē.
neeksistē.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.