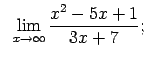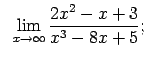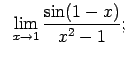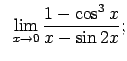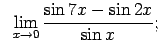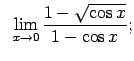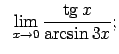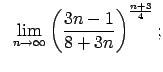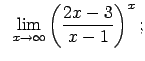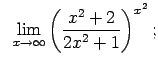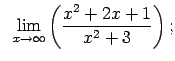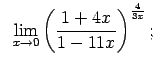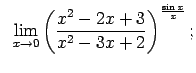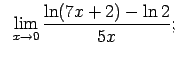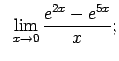Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 8 Bezgalīgi mazas funkcijas un to
Augstāk: vallievads2ht
Previous: 6.2. Funkcijas bezgalīga robeža
Robežu izskaitļošanai izmanto šādas galīgu robežu īpašības.
- Ja eksistē galīga robeža
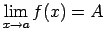
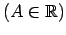 , tad
, tad  ir ierobežota funkcija
punkta
ir ierobežota funkcija
punkta 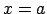 apkārtnē.
apkārtnē.
- Ja funkcija
 ir konstanta punkta
ir konstanta punkta 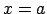 apkārtnē,
t.i., visiem
apkārtnē,
t.i., visiem 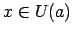
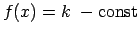 , tad
, tad
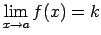 .
.
- Ja funkcijai
 eksistē galīga robeža
eksistē galīga robeža
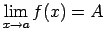 , tad eksistē arī robeža šīs funkcijas modulim
, tad eksistē arī robeža šīs funkcijas modulim 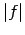 ,
pie tam
,
pie tam
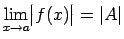 .
.
- Ja
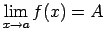
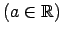 , tad
, tad
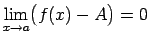 .
.
- Ja eksistē galīgas robežas
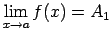 un
un
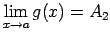 , tad eksistē galīga robeža šo funkciju summai,
pie tam
, tad eksistē galīga robeža šo funkciju summai,
pie tam
- Ja eksistē galīga robeža
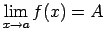 , tad eksistē galīga robeža šīs funkcijas
reizinājumam ar konstanti
, tad eksistē galīga robeža šīs funkcijas
reizinājumam ar konstanti 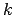 , pie tam
, pie tam
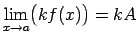 .
.
- Ja funkcija
 definēta un ierobežota punkta
definēta un ierobežota punkta 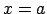 kādā
apkārtnē un funkcijai
kādā
apkārtnē un funkcijai 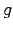 eksistē robeža
eksistē robeža
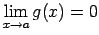 , tad eksistē robeža šo funkciju reizinājumam, pie
tam
, tad eksistē robeža šo funkciju reizinājumam, pie
tam
- Ja eksistē galīgas robežas
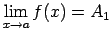 un
un
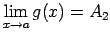 , tad eksistē galīga robeža šo funkciju
reizinājumam, pie tam
, tad eksistē galīga robeža šo funkciju
reizinājumam, pie tam
- Ja eksistē galīgas robežas
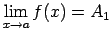 un
un
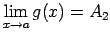 , pie tam
, pie tam 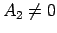 , tad eksistē galīga robeža
funkcijai
, tad eksistē galīga robeža
funkcijai
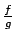 , pie tam
, pie tam
- Ja eksistē robežas
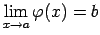 ,
,
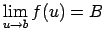 un salikta funkcija
un salikta funkcija
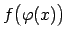 ir
definēta punkta
ir
definēta punkta 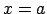 pārdurtā apkārtnē, pie tam šajā apkārtnē
pārdurtā apkārtnē, pie tam šajā apkārtnē
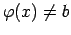 , tad punktā
, tad punktā 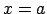 eksistē robeža saliktai
funkcijai
eksistē robeža saliktai
funkcijai
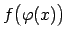 , un šī robeža ir
, un šī robeža ir 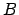 , t.i.,
, t.i.,
Tā kā virkne ir funkcijas īpašs gadījums, tad visas šīs īpašības
ir spēkā arī virknēm.
Var būt gadījumi, kad robežu izskaitļošana, izmantojot iepriekš
uzskaitītās īpašības, nav iespējama.
- Ja
tad robežas
gadījumā 9. īpašību pielietot
nedrīkst un runā par ``
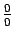 '' veida nenoteiktību.
'' veida nenoteiktību.
- Ja
tad robežas
gadījumā sastopas ar
``
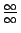 '' veida nenoteiktību.
'' veida nenoteiktību.
- Skaitļojot robežu
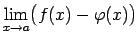 , kur
, kur
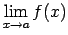 un
un
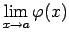 ir bezgalības ar vienādām zīmēm, sastopas ar
``
ir bezgalības ar vienādām zīmēm, sastopas ar
``
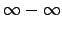 '' veida nenoteiktību.
'' veida nenoteiktību.
- Eksistē nenoteiktības, kas ir sastītas ar
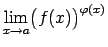 atrašanu
atrašanu
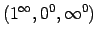 .
.
Nenoteiktības var novērst,
- veicot algebriskus vai trigonometriskus
pārveidojumus (funkciju sadalot reizinātājos vai saskaitāmajos,
vienādojot daļu saucējus, atņemot vai pieskaitot kādu izteiksmi,
dalot un reizinot ar kādu funkciju, iznesot kopīgo reizinātāju pirms iekavām,
utt.),
- atsevišķas funkcijas aizstājot ar ekvivalentām bezgalīgi
mazām funkcijām,
- izmantojot tā saucamās ``ievērojamās robežas'':
-
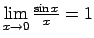 ,
,
-
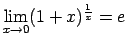 ,
,
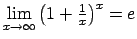 ,
,
-
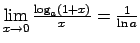 ,
,
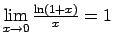 ,
,
-
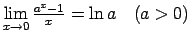 ,
,
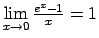 ,
,
-
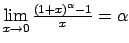 .
.
Nenoteiktību ``
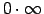 '' viegli var pārveidot par vienu no
nenoteiktībām ``
'' viegli var pārveidot par vienu no
nenoteiktībām ``
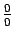 '' vai ``
'' vai ``
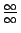 ''.
Piemēram, ja
''.
Piemēram, ja
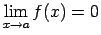 un
un
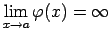 , tad reizinājumu
, tad reizinājumu
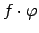 pārveido šādi:
pārveido šādi:
Tādā veidā nenoteiktība ``
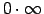 '' tiek pārveidota par
nenoteiktību ``
'' tiek pārveidota par
nenoteiktību ``
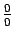 ''.
''.
Nenoteiktību ``
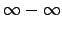 '' var pārveidot par nenoteiktību
``
'' var pārveidot par nenoteiktību
``
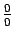 '' šādi:
'' šādi:
Lietojot logaritmēšanu, nenoteiktības ``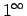 '', ``
'', ``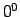 '',
``
'',
``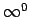 '' var pārveidot par nenoteiktību ``
'' var pārveidot par nenoteiktību ``
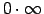 ''.
Par šāda veida nenoteiktību tās var arī pārveidot, uzrakstot
funkciju
''.
Par šāda veida nenoteiktību tās var arī pārveidot, uzrakstot
funkciju 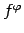 šādi:
šādi:
-
7.1. piem
 rs.
rs.
- Atrast
Tā kā
un
tad šajā piemērā sastopas ar nenoteiktību ``
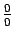 ''.
Lai to novērstu, sadala skaitītāju un saucēju reizinātājos,
saīsina daļu ar
''.
Lai to novērstu, sadala skaitītāju un saucēju reizinātājos,
saīsina daļu ar 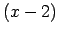 (kas šoreiz tiecas uz 0), un
nenoteiktība tiek novērsta:
(kas šoreiz tiecas uz 0), un
nenoteiktība tiek novērsta:
-
7.2. piem
 rs.
rs.
- Atrast
Šis piemērs satur nenoteiktību ``
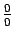 ''. Lai to
novērstu, ``pārnes'' iracionalitāti no daļas skaitītāja uz
saucēju, reizinot skaitītāju un saucēju ar skaitītājam saistīto
izteiksmi, t.i., ar
''. Lai to
novērstu, ``pārnes'' iracionalitāti no daļas skaitītāja uz
saucēju, reizinot skaitītāju un saucēju ar skaitītājam saistīto
izteiksmi, t.i., ar
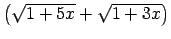 :
:
-
7.3. piem
 rs.
rs.
- Atrast
Šis piemērs satur nenoteiktību ``
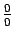 ''. Lai to
novērstu, skaitītāju papildina līdz divu skaitļu kubu
starpībai, reizinot daļas skaitītāju un saucēju ar
''. Lai to
novērstu, skaitītāju papildina līdz divu skaitļu kubu
starpībai, reizinot daļas skaitītāju un saucēju ar
![$ \left(\sqrt[3]{(10-x)^2}+2\sqrt[3]{10-x}+4\right)$](img675.gif) (skat.5; tādā veidā iracionalitāte
no skaitītāja tiek ``pārnesta'' uz saucēju):
(skat.5; tādā veidā iracionalitāte
no skaitītāja tiek ``pārnesta'' uz saucēju):
-
7.4. piem
 rs.
rs.
- Atrast
Šis piemērs satur nenoteiktību ``
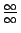 ''. Lai
to novērstu, skaitītāja un saucēja polinomus jādala ar
''. Lai
to novērstu, skaitītāja un saucēja polinomus jādala ar 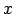 augstāko pakāpi (šoreiz ar
augstāko pakāpi (šoreiz ar 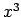 ):
):
-
7.5. piem
 rs.
rs.
- Atrast
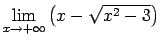 .
.
Šis piemērs satur nenoteiktību ``
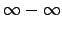 ''. Lai to
novērstu, doto funkciju reizina un dala ar tās saistīto
izteiksmi, t.i., ar
''. Lai to
novērstu, doto funkciju reizina un dala ar tās saistīto
izteiksmi, t.i., ar
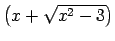 :
:
-
7.6. piem
 rs.
rs.
- Atrast
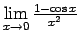 .
.
Šis piemērs satur nenoteiktību ``
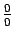 ''. Lai to
novērstu, iepriekš izsakot
''. Lai to
novērstu, iepriekš izsakot
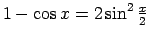 ,
izmanto pirmo ievērojamo robežu, t.i.,
,
izmanto pirmo ievērojamo robežu, t.i.,
-
7.7. piem
 rs.
rs.
- Atrast
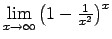 .
.
Šis piemērs satur nenoteiktību ``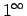 ''. Lai to novērstu,
izmanto otro ievērojamo robežu, t.i.,
(skat. 6).
''. Lai to novērstu,
izmanto otro ievērojamo robežu, t.i.,
(skat. 6).
-
7.8. piem
 rs.
rs.
- Atrast
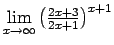 .
.
Šis piemērs satur nenoteiktību ``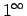 ''. lai to novērstu,
izmanto otro ievērojamo robežu. Uzdevumu var atrisināt ar
diviem paņēmieniem.
''. lai to novērstu,
izmanto otro ievērojamo robežu. Uzdevumu var atrisināt ar
diviem paņēmieniem.
1. paņēmiens.
2. paņēmiens.
-
7.9. piem
 rs.
rs.
- Atrast
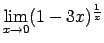 .
.
Šis piemērs satur nenoteiktību ``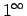 ''. Lai to novērstu,
izmanto otro ievērojamo robežu, šoreiz
''. Lai to novērstu,
izmanto otro ievērojamo robežu, šoreiz
-
7.10. piem
 rs.
rs.
- Atrast
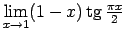 .
.
Šis piemērs satur nenoteiktību ``
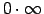 ''.
''.
(skat. 7)
-
7.11. piem
 rs.
rs.
- Atrast
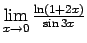 .
.
Šis piemērs satur nenoteiktību ``
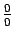 ''. Lai to
novērstu, lieto robežu
''. Lai to
novērstu, lieto robežu
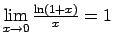 un pirmo
ievērojamo robežu:
un pirmo
ievērojamo robežu:
Auditorijā risināmie uzdevumi
Atrast robežas
Mājas darba uzdevumi
Atrast robežas



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 8 Bezgalīgi mazas funkcijas un to
Augstāk: vallievads2ht
Previous: 6.2. Funkcijas bezgalīga robeža
2003-05-15
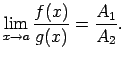
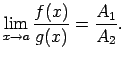
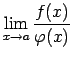
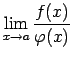
![]() ,
,
![]() ,
,
![]() ,
,
![]() '' viegli var pārveidot par vienu no
nenoteiktībām ``
'' viegli var pārveidot par vienu no
nenoteiktībām ``
![]() '' vai ``
'' vai ``
![]() ''.
Piemēram, ja
''.
Piemēram, ja
![]() un
un
![]() , tad reizinājumu
, tad reizinājumu
![]() pārveido šādi:
pārveido šādi:
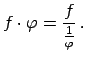
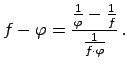
![]() '', ``
'', ``![]() '',
``
'',
``![]() '' var pārveidot par nenoteiktību ``
'' var pārveidot par nenoteiktību ``
![]() ''.
Par šāda veida nenoteiktību tās var arī pārveidot, uzrakstot
funkciju
''.
Par šāda veida nenoteiktību tās var arī pārveidot, uzrakstot
funkciju ![]() šādi:
šādi:
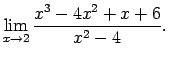
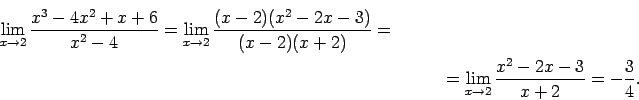
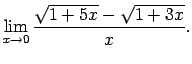
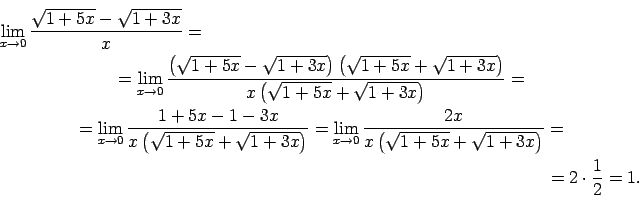
![$\displaystyle \lim\limits_{x\rightarrow 2}\frac{\sqrt[3]{10-x}-2}{x-2}\/.$](img674.gif)
![\begin{multline*}
\lim\limits_{x\rightarrow 2}\frac{\sqrt[3]{10-x}-2}{x-2}
=\l...
...sqrt[3]{10-x}\right)^2+
2\sqrt[3]{10-x}+4\Bigr)}=-\frac{1}{12}.
\end{multline*}](img677.gif)
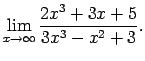
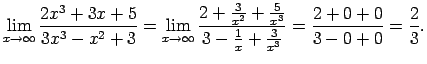
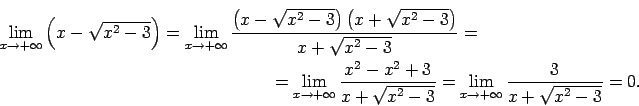
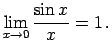
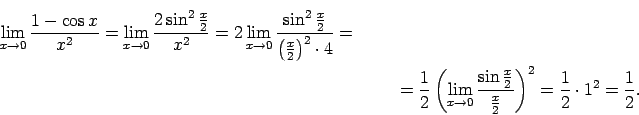
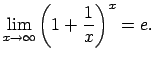
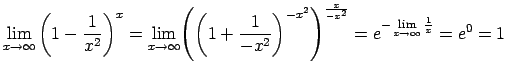
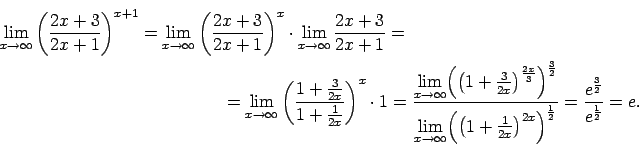
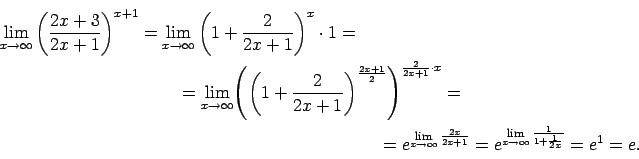
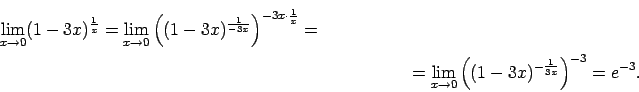
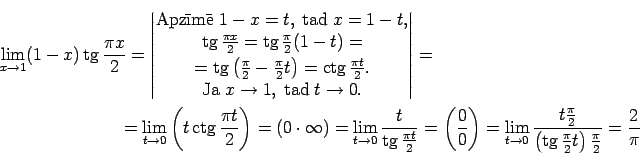
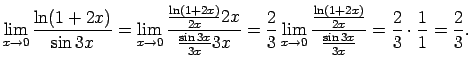
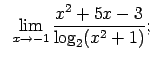
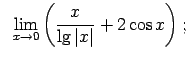
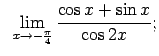
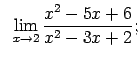
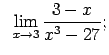
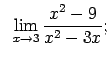
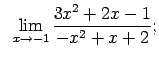
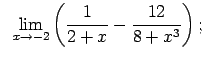
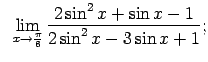
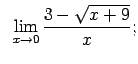
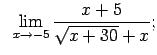
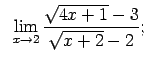
![$\displaystyle \;\;\lim\limits_{x\rightarrow -2}\frac{\sqrt[3]{x-6}+2}{2+x};$](img720.gif)
![$\displaystyle \;\;\lim\limits_{x\rightarrow 1}\frac{\sqrt[3]{x}-1}{\sqrt{x}-1};$](img722.gif)
![$\displaystyle \;\;\lim\limits_{x\rightarrow 0}\frac{\sqrt{1+x}-1}{\sqrt[3]{1+x}-1};$](img724.gif)
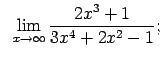
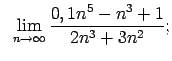
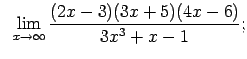
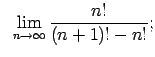
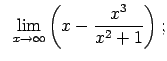
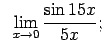
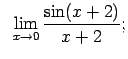
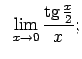
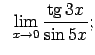
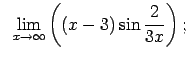
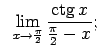
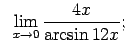
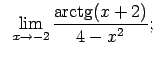
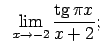
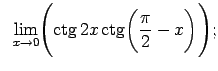
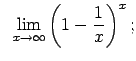
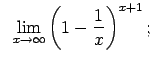
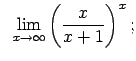
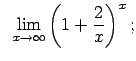
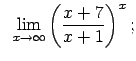
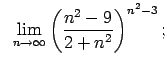
![$\displaystyle \;\;\lim\limits_{x\rightarrow\infty}\sqrt[3]{\left(\frac{3x-4} {3x+2}\right)^x\left(\frac{3x-4}{3x+2}\right)};$](img780.gif)
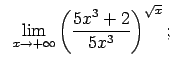
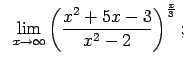
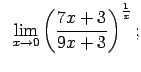
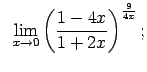
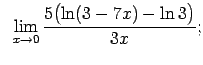
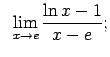
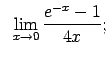
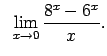
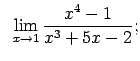
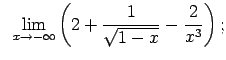
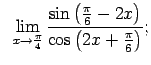
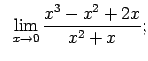
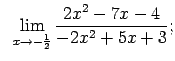
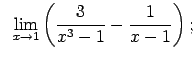
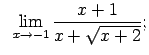
![$\displaystyle \;\;\lim\limits_{x\rightarrow 0}\frac{\sqrt[3]{1-x^2}-1}{x^2-3x};$](img820.gif)
![$\displaystyle \;\;\lim\limits_{x\rightarrow 64}\frac{\sqrt{x}-8}{4-\sqrt[3]{x}};$](img821.gif)