


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 7. Robežu izskaitļošana
Augstāk: 6. Funkcijas robeža
Previous: 6.1. Funkcijas galīga robeža
Apskata gadījumu, kad
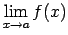 ir
bezgalība. Atkarībā no tā, vai
ir
bezgalība. Atkarībā no tā, vai 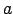 ir skaitlis vai viens no
simboliem ``bezgalība'' (plus bezgalība, mīnus bezgalība,
bezgalība bez zīmes), ir iespējami 12 gadījumi.
ir skaitlis vai viens no
simboliem ``bezgalība'' (plus bezgalība, mīnus bezgalība,
bezgalība bez zīmes), ir iespējami 12 gadījumi.
Piemēram,
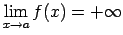 ,
,
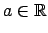 .
.
Šoreiz simbolu 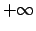 sauc par funkcijas
sauc par funkcijas 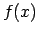 robežu
punktā
robežu
punktā 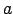 , ja jebkuram skaitlim
, ja jebkuram skaitlim 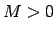 eksistē tāds
eksistē tāds
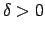 , ka visiem
, ka visiem 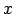 , kuriem
, kuriem
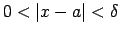 , izpildās
nevienādība
, izpildās
nevienādība 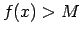 .
.
Ģeometriski tas nozīmē: lai cik liels arī nebūtu skaitlis 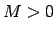 ,
eksistē tāds intervāls
,
eksistē tāds intervāls
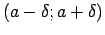 , ka visiem
, ka visiem 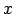 no šī
intervāla funkcijas grafiks atrodas virs taisnes
no šī
intervāla funkcijas grafiks atrodas virs taisnes 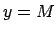 (6.3. zīm.).
(6.3. zīm.).
Piemēram,
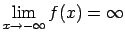 .
.
Šoreiz simbolu 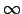 sauc par funkcijas
sauc par funkcijas 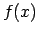 robežu
punktā
robežu
punktā 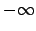 , ja jebkuram skaitlim
, ja jebkuram skaitlim 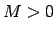 eksistē tāds
skaitlis
eksistē tāds
skaitlis 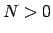 , ka visiem
, ka visiem 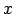 , kuriem
, kuriem 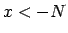 , izpildās nevienādība
, izpildās nevienādība
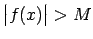 .
.
Ģeometriski tas nozīmē: lai cik liels arī nebūtu 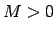 , eksistē
tāds intervāls
, eksistē
tāds intervāls
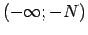 , ka visiem
, ka visiem 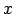 , kas pieder šim
intervālam, funkcijas grafiks atrodas zem taisnes
, kas pieder šim
intervālam, funkcijas grafiks atrodas zem taisnes 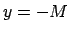 vai virs
taisnes
vai virs
taisnes 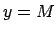 .
.
-
6.3. piem
 rs.
rs.
- Lietojot funkcijas robežas definīciju,
pierādīt, ka
Skaitlim
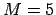 atrast atbilstošo
atrast atbilstošo
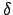 .
.
Izvēlas patvaļīgu skaitli 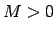 , apskata nevienādību
un atrisina to attiecībā pret
, apskata nevienādību
un atrisina to attiecībā pret
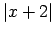 :
Tādējādi
:
Tādējādi
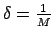 .
.
Kādu arī neizvēlētos 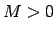 , eksistē
, eksistē
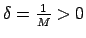 , ka
visiem
, ka
visiem 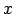 , kuriem
, kuriem
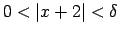 , izpildās nevienādība
Tādējādi
Ja
, izpildās nevienādība
Tādējādi
Ja 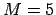 , tad
, tad
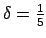 .
.
Ģeometriski tas nozīmē, ka visiem 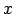 , kas pieder intervālam
funkcijas grafiks atrodas zem taisnes
, kas pieder intervālam
funkcijas grafiks atrodas zem taisnes 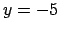 vai virs taisnes
vai virs taisnes
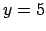 (6.4. zīm.).
(6.4. zīm.).
-
6.4. piem
 rs.
rs.
- Lietojot funkcijas robežas definīciju,
pierādīt, ka
Izvēlas patvaļīgu skaitli
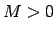 , apskata nevienādību
un atrisina to attiecībā pret
, apskata nevienādību
un atrisina to attiecībā pret 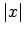 :
tādējādi
Kādu arī neizvēlētos
:
tādējādi
Kādu arī neizvēlētos 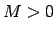 , eksistē tāds
, eksistē tāds
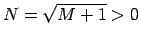 ,
ka visiem
,
ka visiem 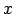 , kuriem
, kuriem
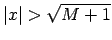 , izpildās nevienādība:
Tādējādi
(6.5. zīm.).
, izpildās nevienādība:
Tādējādi
(6.5. zīm.).
Auditorijā risināmie uzdevumi
Lietojot funkcijas robežas definīciju, pierādīt:
Mājas darba uzdevumi
Lietojot funkcijas robežas definīciju, pierādīt:



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 7. Robežu izskaitļošana
Augstāk: 6. Funkcijas robeža
Previous: 6.1. Funkcijas galīga robeža
2003-05-15
![]() ir
bezgalība. Atkarībā no tā, vai
ir
bezgalība. Atkarībā no tā, vai ![]() ir skaitlis vai viens no
simboliem ``bezgalība'' (plus bezgalība, mīnus bezgalība,
bezgalība bez zīmes), ir iespējami 12 gadījumi.
ir skaitlis vai viens no
simboliem ``bezgalība'' (plus bezgalība, mīnus bezgalība,
bezgalība bez zīmes), ir iespējami 12 gadījumi.
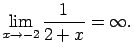
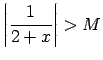
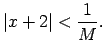
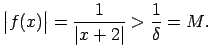
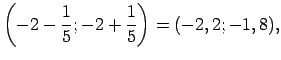
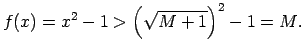
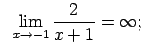
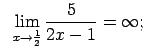
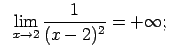
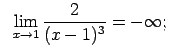
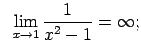
![$\displaystyle \;\;\lim\limits_{x\rightarrow 1}\frac{1}{\sqrt[3]{(x-1)^2}}=+\infty;$](img598.gif)
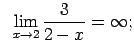
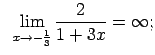
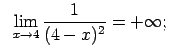
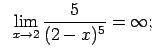
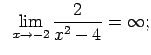
![$\displaystyle \;\;\lim\limits_{x\rightarrow -1}\frac{1}{\sqrt[3]{(1+x)^2}}=+\infty;$](img609.gif)