


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 6.2. Funkcijas bezgalīga robeža
Augstāk: 6. Funkcijas robeža
Previous: 6. Funkcijas robeža
-
6.1. definīcija.
- Skaitli
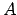 sauc par funkcijas
sauc par funkcijas  robežu punktā
robežu punktā
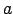
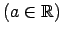 , ja jebkuram
, ja jebkuram
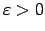 eksistē tāds
eksistē tāds 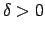 (atkarīgs no
(atkarīgs no
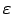 ), ka visiem
), ka visiem 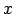 , kuriem
, kuriem
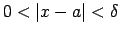 ,
izpildās nevienādība
,
izpildās nevienādība
No ģeometriskā viedokļa tas nozīmē: lai cik šaura arī nebūtu
horizontālā josla starp taisnēm
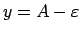 un
un
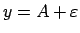 , funkcijas grafiks, izņemot varbūt punktu
, funkcijas grafiks, izņemot varbūt punktu
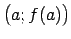 , visiem
, visiem
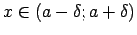 atrodas
šajā joslā (6.1. zīm.).
atrodas
šajā joslā (6.1. zīm.).
Raksta:
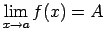 .
.
-
6.1. piem
 rs.
rs.
- Lietojot funkcijas robežas definīciju,
pierādīt, ka
Skaitlim
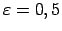 atrast atbilstošo
atrast atbilstošo 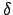 . Sniegt
ģeometrisko interpretāciju.
. Sniegt
ģeometrisko interpretāciju.
Pārveido starpību
Atrisina nevienādību
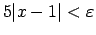 attiecībā pret
attiecībā pret
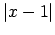 :
Tādējādi var ņemt
:
Tādējādi var ņemt
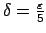 .
.
Tātad jebkuram
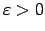 eksistē tam
atbilstošais
eksistē tam
atbilstošais
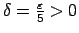 , ka visiem
, ka visiem 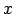 ,
kuriem
,
kuriem
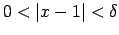 , t.i.,
, t.i.,
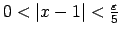 , izpildās nevienādība
Saskaņā ar funkcijas robežas definīciju
, izpildās nevienādība
Saskaņā ar funkcijas robežas definīciju
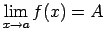
Ja
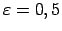 , tad
, tad
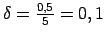 .
.
-
6.2. piem
 rs.
rs.
- Lietojot funkcijas robežas definīciju,
pierādīt, ka
Skaitlim
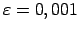 atrast atbilstošo
atrast atbilstošo 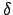 .
.
Pārveido starpību
Atrisina nevienādību
attiecībā pret 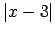 .
.
Ja 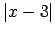 apzīmē ar
apzīmē ar 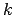 , tad iegūst nevienādību
Atbilstošā kvadrātvienādojuma
saknes ir
, tad iegūst nevienādību
Atbilstošā kvadrātvienādojuma
saknes ir
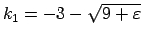 un
un
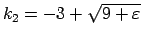 .
.
Nevienādības
atrisinājums ir
Tādējādi
Tā kā
tad
Tātad var ņemt
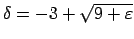 .
.
Kādu arī neizvēlētos
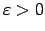 , eksistē tam atbilstošais
, eksistē tam atbilstošais
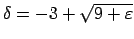 , ka visiem
, ka visiem 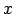 , kuriem
izpildās nevienādība
Saskaņā ar funkcijas robežas definīciju
, kuriem
izpildās nevienādība
Saskaņā ar funkcijas robežas definīciju
Auditorijā risināmie uzdevumi
Lietojot funkcijas robežas definīciju, pierādīt dotās vienādības.
Skaitlim
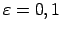 atrast atbilstošo
atrast atbilstošo 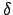 .
.
-
- Lietojot funkcijas robežas definīciju, pārbaudīt, vai
ir pareiza vienādība
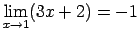 .
.
Mājas darba uzdevumi
Lietojot funkcijas robežas definīciju, pierādīt dotās vienādības.
Skaitlim
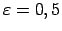 atrast atbilstošo
atrast atbilstošo 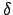 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 6.2. Funkcijas bezgalīga robeža
Augstāk: 6. Funkcijas robeža
Iepriekšējais: 6. Funkcijas robeža
2003-05-15
![]() un
un
![]() , funkcijas grafiks, izņemot varbūt punktu
, funkcijas grafiks, izņemot varbūt punktu
![]() , visiem
, visiem
![]() atrodas
šajā joslā (6.1. zīm.).
atrodas
šajā joslā (6.1. zīm.).
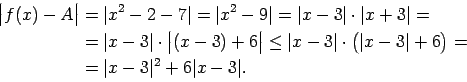
![]() atrast atbilstošo
atrast atbilstošo ![]() .
.
![]() atrast atbilstošo
atrast atbilstošo ![]() .
.