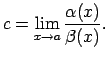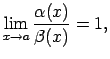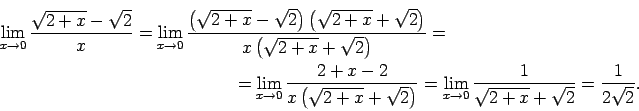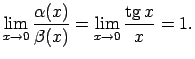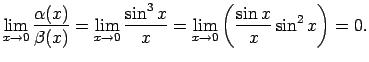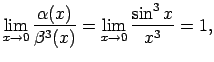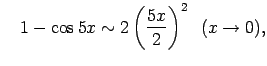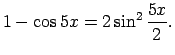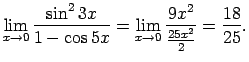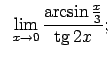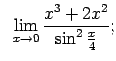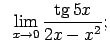Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 9. Nepārtrauktas funkcijas
Augstāk: vallievads2ht
Previous: 7. Robežu izskaitļošana
-
8.1. definīcija.
- Funkciju
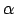 sauc par bezgalīgi mazu
funkciju punktā
sauc par bezgalīgi mazu
funkciju punktā 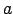 , ja
, ja
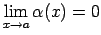 .
.
Pieņemsim, ka 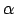 un
un 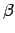 ir bezgalīgi mazas funkcijas
punktā
ir bezgalīgi mazas funkcijas
punktā 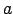 .
.
Apzīmē
- Ja
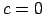 , tad
, tad 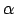 sauc par augstākas kārtas
bezgalīgi mazu funkciju, salīdzinot ar
sauc par augstākas kārtas
bezgalīgi mazu funkciju, salīdzinot ar 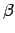 , kad
, kad
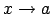 , un raksta:
, un raksta:
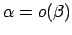 (skat. 8).
(skat. 8).
- Ja
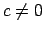 , un
, un
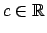 , tad
, tad 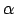 ,
, 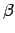 sauc par vienādas
kārtas bezgalīgi mazām funkcijām, kad
sauc par vienādas
kārtas bezgalīgi mazām funkcijām, kad
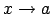 .
.
Pie tam, ja 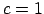 , t.i., ja
tad
, t.i., ja
tad 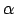 un
un 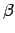 sauc par ekvivalentām bezgalīgi mazām
funkcijām, kad
sauc par ekvivalentām bezgalīgi mazām
funkcijām, kad
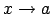 , un raksta:
, un raksta:
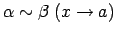 .
.
-
8.2. definīcija.
- Funkciju
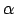 sauc par
sauc par 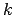 -tās kārtas
bezgalīgi mazu funkciju, salīdzinot ar bezgalīgi mazu funkciju
-tās kārtas
bezgalīgi mazu funkciju, salīdzinot ar bezgalīgi mazu funkciju
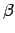 , kad
, kad
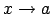 , ja
, ja 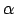 un
un 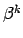 ir
vienādas kārtas bezgalīgi mazas funkcijas, kad
ir
vienādas kārtas bezgalīgi mazas funkcijas, kad
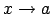 .
.
-
8.1. piem
 rs.
rs.
- Salīdzināt bezgalīgi mazas funkcijas:
-
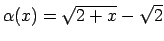 un
un
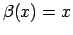 , kad
, kad
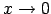 ;
;
-
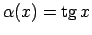 un
un
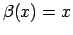 , kad
, kad
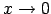 ;
;
-
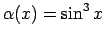 un
un
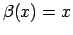 , kad
, kad
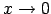 .
.
- Atrodam doto bezgalīgi mazo funkciju attiecības
robežu, kad
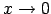 :
:
Tātad dotās funkcijas ir vienādas kārtas bezgalīgi mazas
funkcijas, kad
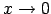 .
.
- Atrod
Dotās funkcijas ir ekvivalentas bezgalīgi mazas funkcijas,
kad
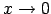 , t.i.,
, t.i.,
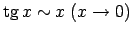 .
.
- Atrod
Funkcija
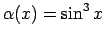 ir augstākas kārtas bezgalīgi
maza funkcija, salīdzinot ar
ir augstākas kārtas bezgalīgi
maza funkcija, salīdzinot ar
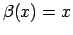 , kad
, kad
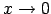 .
.
Tā kā
tad 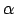 ir 3. kārtas bezgalīgi maza funkcija,
salīdzinot ar
ir 3. kārtas bezgalīgi maza funkcija,
salīdzinot ar 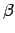 , kad
, kad
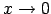 .
.
Izskaitļojot robežas, dažkārt ir izdevīgi bezgalīgi mazās
funkcijas aizstāt ar tām ekvivalentām funkcijām. Tāda pieeja
vienkāršo robežu atrašanu.
-
8.2. piem
 rs.
rs.
- Atrast robežu
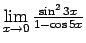 .
.
Piemērā ir dota divu bezgalīgi mazu funkciju
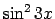 un
un 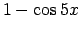 , kad
, kad
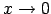 , attiecība. Lai atrastu šo
robežu, šīs bezgalīgi mazās funkcijas, kad
, attiecība. Lai atrastu šo
robežu, šīs bezgalīgi mazās funkcijas, kad
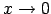 ,
aizstāj ar tām ekvivalentām bezgalīgi mazām funkcijām:
,
aizstāj ar tām ekvivalentām bezgalīgi mazām funkcijām:
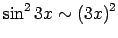
un
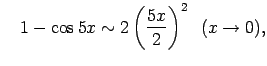
jo
Tādējādi
Auditorijā risināmie uzdevumi
- Salīdzināt bezgalīgi mazo funkciju
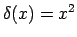 , kad
, kad
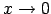 , ar šādām bezgalīgi mazām funkcijām:
, ar šādām bezgalīgi mazām funkcijām:
-
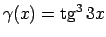 ;
;
-
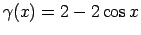 ;
;
-
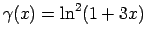 .
.
- Pierādīt, ka dotās bezgalīgi mazās funkcijas norādītajos punktos ir ekvivalentas:
-
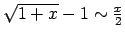 , kad
, kad
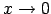 ;
;
-
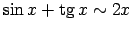 , kad
, kad
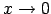 ;
;
-
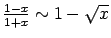 , kad
, kad
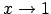 .
.
- Atrast robežas:
-
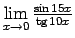 ;
;
-
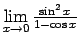 ;
;
-
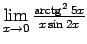 ;
;
-
![$ \lim\limits_{x\rightarrow
0}\frac{\arcsin\sqrt[3]{x^4}}{x\sqrt{x}}$](img888.gif) .
.
Mājas darba uzdevumi
Atrast robežas



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 9. Nepārtrauktas funkcijas
Augstāk: vallievads2ht
Previous: 7. Robežu izskaitļošana
2003-05-15
![]() un
un ![]() ir bezgalīgi mazas funkcijas
punktā
ir bezgalīgi mazas funkcijas
punktā ![]() .
.