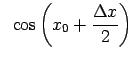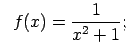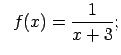Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 10. Vienpusējās robežas, to izskaitļošana. Funkcijas
Augstāk: vallievads2ht
Previous: 8 Bezgalīgi mazas funkcijas un to
-
9.1. definīcija.
- Funkciju
 sauc par nepārtrauktu punktā
sauc par nepārtrauktu punktā
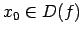 , ja
, ja
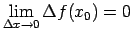 , kur
ir funkcijas
, kur
ir funkcijas  pieaugums punktā
pieaugums punktā 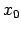 .
.
-
9.2. definīcija.
- Funkciju
 sauc par nepārtrauktu kopā
sauc par nepārtrauktu kopā
 , ja tā ir nepārtraukta šīs kopas katrā punktā.
, ja tā ir nepārtraukta šīs kopas katrā punktā.
-
9.3. definīcija.
- Funkciju, kas ir nepārtraukta savā definīcijas
apgabalā, sauc par nepārtrauktu funkciju.
-
9.1. piem
 rs.
rs.
- Pierādīt, ka funkcija
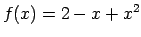 ir
nepārtraukta punktā
ir
nepārtraukta punktā 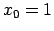 .
.
Atrod
saskaņā ar definīciju funkcija
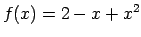 ir nepārtraukta punktā
ir nepārtraukta punktā 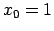 .
.
Ja ir jāpierāda funkcijas nepārtrauktība kādā kopā (vai
definīcijas apgabalā), tad izvēlas patvaļīgu šīs kopas
punktu 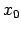 un pierāda funkcijas nepārtrauktību šajā punktā.
un pierāda funkcijas nepārtrauktību šajā punktā.
-
9.2. piem
 rs.
rs.
- Pierādīt, ka
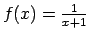 ir nepārtraukta
funkcija.
ir nepārtraukta
funkcija.
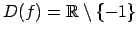 . Izvēlas patvaļīgu
. Izvēlas patvaļīgu
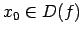 , atrod
, atrod
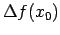 :
:
Tad
Tā kā 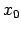 ir patvaļīgs
funkcijas definīcijas apgabala punkts, tad funkcija
ir patvaļīgs
funkcijas definīcijas apgabala punkts, tad funkcija  ir
nepārtraukta funkcija.
ir
nepārtraukta funkcija.
-
9.3. piem
 rs.
rs.
- Pierādīt, ka
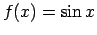 ir nepārtraukta
funkcija.
ir nepārtraukta
funkcija.
Pieņem, ka
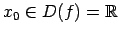 .
Atrod
jo
.
Atrod
jo
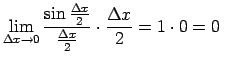
un
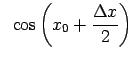
ir
ierobežota funkcija.
Tātad
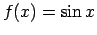 ir nepārtraukta funkcija.
ir nepārtraukta funkcija.
Auditorijā risināmie uzdevumi
Pierādīt, ka dotās funkcijas ir nepārtrauktas.
Mājas darba uzdevumi
Pierādīt, ka dotās funkcijas ir nepārtrauktas.



 Matemātika
DU TSC
Matemātika
DU TSC
Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 10. Vienpusējās robežas, to izskaitļošana. Funkcijas
Augstāk: vallievads2ht
Previous: 8 Bezgalīgi mazas funkcijas un to
2003-05-15
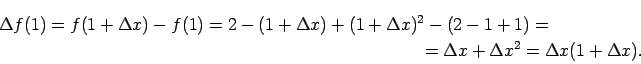
![]() un pierāda funkcijas nepārtrauktību šajā punktā.
un pierāda funkcijas nepārtrauktību šajā punktā.
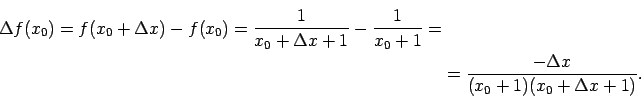
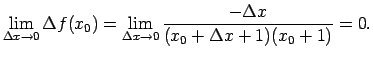
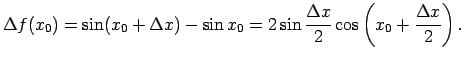
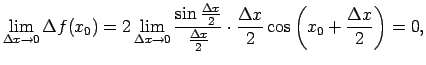
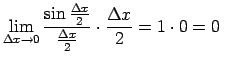 un
un