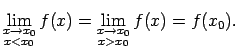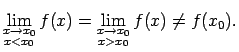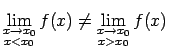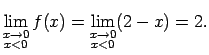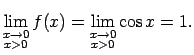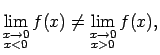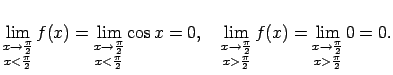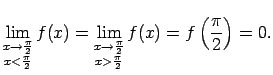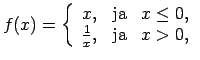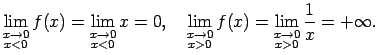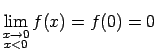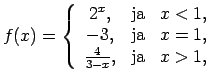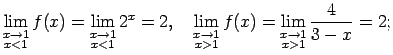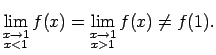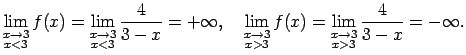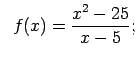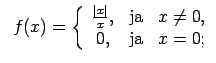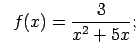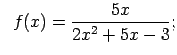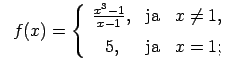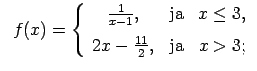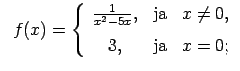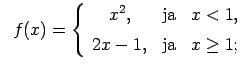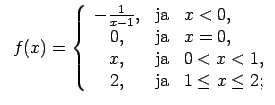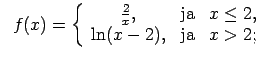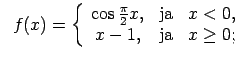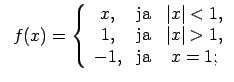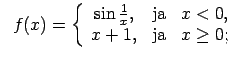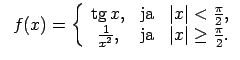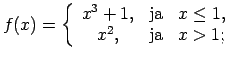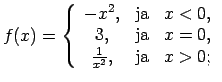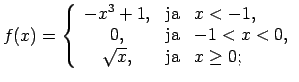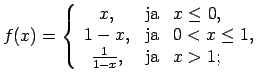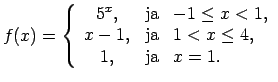Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 11. Pielikums
Augstāk: 10. Vienpusējās robežas, to izskaitļošana. Funkcijas
Previous: 10.1. Funkcijas vienpusējās robežas
No punktā nepārtrauktas funkcijas definīcijas seko, ka funkcija ir
nepārtraukta punktā
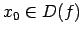 tad un tikai tad, ja
tad un tikai tad, ja
-
10.3. definīcija.
- Punktu
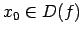 sauc par funkcijas
pārtraukuma punktu, ja šajā punktā funkcija nav
nepārtraukta.
sauc par funkcijas
pārtraukuma punktu, ja šajā punktā funkcija nav
nepārtraukta.
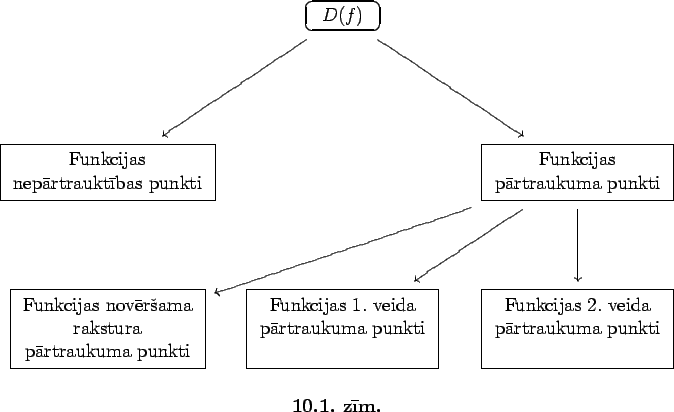
Tātad visi funkcijas definīcijas apgabala punkti iedalās funkcijas
pārtraukuma un nepārtrauktības punktos.
-
10.4. definīcija.
- Funkcijas pārtraukuma punktu
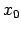 sauc par tās
novēršama rakstura pārtraukuma punktu, ja punktā
sauc par tās
novēršama rakstura pārtraukuma punktu, ja punktā
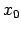 eksistē galīgas un vienādas funkcijas vienpusējās robežas,
bet tās nav vienādas ar funkcijas vērtību šinī punktā, t.i.,
eksistē galīgas un vienādas funkcijas vienpusējās robežas,
bet tās nav vienādas ar funkcijas vērtību šinī punktā, t.i.,
-
10.5. definīcija.
- Funkcijas pārtraukuma punktu
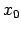 sauc par tās
1. veida pārtraukuma punktu, ja punktā
sauc par tās
1. veida pārtraukuma punktu, ja punktā 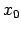 eksistē
galīgas un dažādas funkcijas vienpusējās robežas, t.i.,
(skat.
9).
eksistē
galīgas un dažādas funkcijas vienpusējās robežas, t.i.,
(skat.
9).
-
10.6. definīcija.
- Funkcijas pārtraukuma punktu, kas nav ne
funkcijas novēršama rakstura pārtraukuma punkts, ne funkcijas
1. veida pārtraukuma punkts, sauc par funkcijas 2. veida
pārtraukuma punktu.
Tātad funkcijas II veida pārtraukuma punkti ir funkcijas tie
pārtraukuma punkti, kuros vismaz viena no šīs funkcijas
vienpusējām robežām ir bezgalīga vai neeksistē.
Uzskatāmības labad var izveidot šādu shēmu:
-
10.2. piem
 rs.
rs.
- Atrast funkcijas
pārtraukuma punktus un noteikt to veidu. Konstruēt funkcijas
shematisku grafiku.
Dotās funkcijas definīcijas apgabals
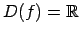 .
.
Katrā no intervāliem
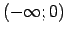 ,
,
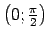 ,
,
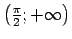 funkcija ir nepārtraukta, jo
ir uzdota ar nepārtrauktām funkcijām, atbilstoši
funkcija ir nepārtraukta, jo
ir uzdota ar nepārtrauktām funkcijām, atbilstoši 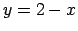 ,
,
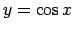 ,
, 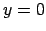 .
.
Atliek izpētīt funkcijas raksturu punktos 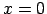 un
un
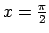 .
.
Atrod vienpusējās robežas funkcijai punktā 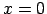 .
.
Tā kā 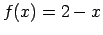 , kad
, kad 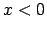 , tad
Tā kā
, tad
Tā kā
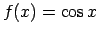 , kad
, kad
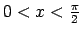 , tad
Šoreiz
tāpēc
, tad
Šoreiz
tāpēc 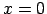 ir funkcijas I veida pārtraukuma punkts.
ir funkcijas I veida pārtraukuma punkts.
Atrod vienpusējās robežas funkcijai punktā
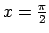 :
:
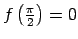 .
.
Funkcija ir
nepārtraukta punktā
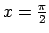 , jo
Atzīmēsim, ka punktā
, jo
Atzīmēsim, ka punktā 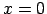 funkcija ir nepārtraukta no kreisās puses (10.2. zīm.).
funkcija ir nepārtraukta no kreisās puses (10.2. zīm.).
-
10.3. piem
 rs.
rs.
- Atrast funkcijas
pārtraukuma punktus un noteikt to veidu. Konstruēt funkcijas
shematisku grafiku.
10.3. piemērā dotās funkcijas definīcijas apgabals
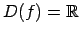 . Katrā no intervāliem
. Katrā no intervāliem
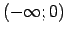 un
un
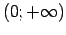 funkcija ir nepārtraukta.
funkcija ir nepārtraukta.
Atrod vienpusējās robežas funkcijai punktā 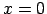 :
Pie tam,
:
Pie tam, 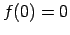 , tātad punkts
, tātad punkts
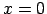 ir funkcijas
ir funkcijas 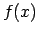 2. veida pārtraukuma punkts.
2. veida pārtraukuma punkts.
Arī šoreiz punktā 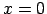 funkcija ir nepārtraukta no kreisās puses,
jo
(skat. 10.3. zīm.).
funkcija ir nepārtraukta no kreisās puses,
jo
(skat. 10.3. zīm.).
-
10.4. piem
 rs.
rs.
- Atrast funkcijas
pārtraukuma punktus un noteikt to veidu. Konstruēt funkcijas
shematisku grafiku.
10.4. piemērā dotās funkcijas
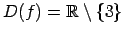 .
.
Šoreiz atrod funkcijas vienpusējās robežas punktos 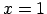 un
un 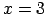 .
.
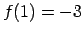 .
.
Tātad
Punkts 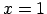 ir funkcijas novēršama rakstura pārtraukuma punkts.
Punkts
ir funkcijas novēršama rakstura pārtraukuma punkts.
Punkts 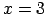 nav funkcijas
pārtraukuma punkts, jo tas nepieder tās definīcijas apgabalam.
Dotās funkcijas shematisks grafiks ir attēlots 10.4. zīm.
nav funkcijas
pārtraukuma punkts, jo tas nepieder tās definīcijas apgabalam.
Dotās funkcijas shematisks grafiks ir attēlots 10.4. zīm.
Auditorijā risināmie uzdevumi
- Lietojot funkciju shematiskus grafikus, izpētīt
funkcijas raksturu punktā
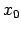 .
.
- Atrast funkciju pārtraukuma punktus un noteikt to veidu;
konstruēt funkciju shematiskus grafikus.
 a a |
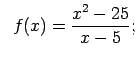 |
 b b |
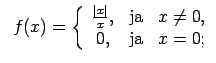 |
|
 c c |
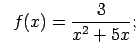 |
 d d |
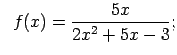 |
|
 e e |
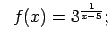 |
 f f |
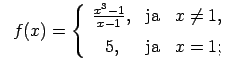 |
|
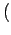 g g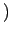 |
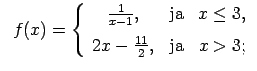 |
 h h |
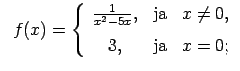 |
|
 i i |
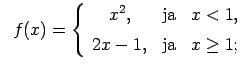 |
 j j |
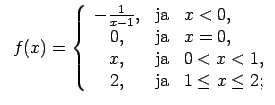 |
|
 k k |
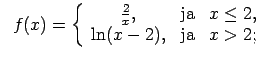 |
 l l |
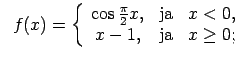 |
|
 m m |
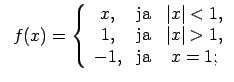 |
 n n |
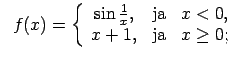 |
|
 0 0 |
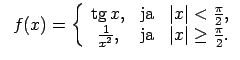 |
|
|
Mājas darba uzdevumi
Atrast funkciju pārtraukuma punktus un noteikt to veidu. Konstruēt
shematisku funkcijas grafiku.
-
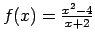 ;
;
-
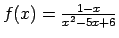 ;
;
-
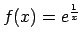 ;
;
-

-
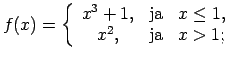
-
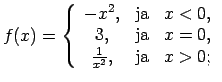
-
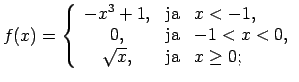
-

-
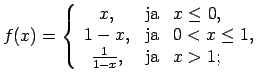
-
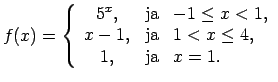



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 11. Pielikums
Augstāk: 10. Vienpusējās robežas, to izskaitļošana. Funkcijas
Previous: 10.1. Funkcijas vienpusējās robežas
2003-05-15
![]() tad un tikai tad, ja
tad un tikai tad, ja