I.1.Konstruēt funkciju grafikus.
I.2.Atrisināt vienādojumus.
I.3.Atrisināt nevienādības.
II.Noteikt ar formulu uzdotās funkcijas definīcijas apgabalu.
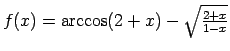 ;
;
![$ f(x)=\frac{1}{\sqrt[5]{3x-4}}+\sqrt{\lg\frac{3x}{5-2x}}$](img1103.gif) ;
;
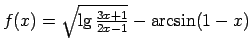 ;
;
![$ f(x)=\sqrt[3]{\frac{1}{3x-2}}+\frac{\sqrt{2x+5}}{\log_2(3-x)}$](img1107.gif) ;
;
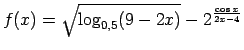 ;
;
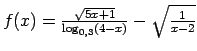 ;
;
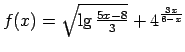 ;
;
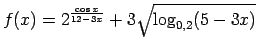 ;
;
![$ f(x)=\sqrt[4]{\log_{0,3}(1-4x)}+2\arctg\frac{\sqrt[3]{8-3x}}{24x^2-1}$](img1116.gif) ;
;
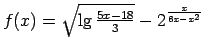 ;
;
III.Noteikt, kuras no dotajām funkcijām ir pāra funkcijas,
kuras - nepāra funkcijas.
IV.Noteikt, vai dotās funkcijas ir periodiskas un noteikt
periodu.
V. Katrai no dotajām funkcijām atrast apvērsto funkciju un
noteikt apvērstās funkcijas definīcijas un vērtību apgabalu.
VI.Lietojot virknes robežas definīciju, pierādīt, ka
![]() . Skaitlim
. Skaitlim
![]() atrast atbilstošo
atrast atbilstošo ![]() .
.
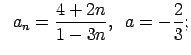 |
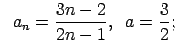 |
|||
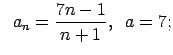 |
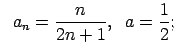 |
|||
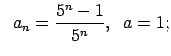 |
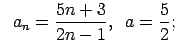 |
|||
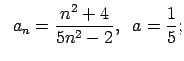 |
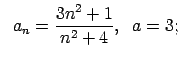 |
|||
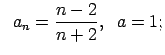 |
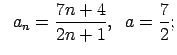 |
|||
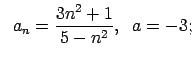 |
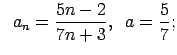 |
|||
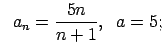 |
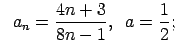 |
|||
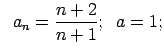 |
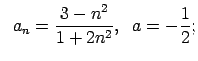 |
|||
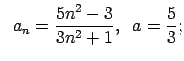 |
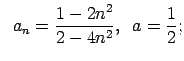 |
|||
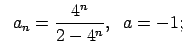 |
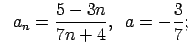 |
|||
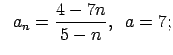 |
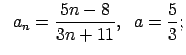 |
|||
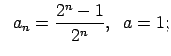 |
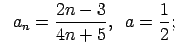 |
|||
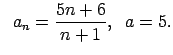 |
VII.Lietojot funkcijas robežas definīciju, pierādīt, ka
![]() . Skaitlim
. Skaitlim
![]() atrast atbilstošo
atrast atbilstošo ![]() .
.
VIII.1.Atrast robežas.
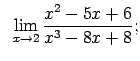 |
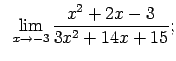 |
|||
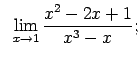 |
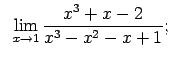 |
|||
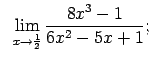 |
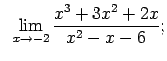 |
|||
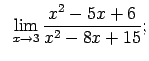 |
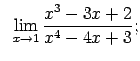 |
|||
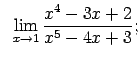 |
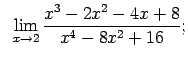 |
|||
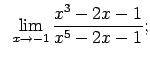 |
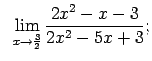 |
|||
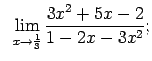 |
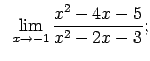 |
|||
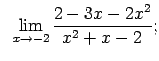 |
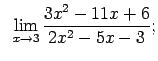 |
|||
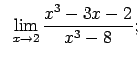 |
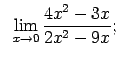 |
|||
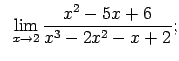 |
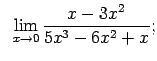 |
|||
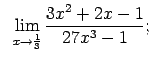 |
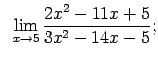 |
|||
 |
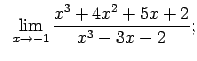 |
|||
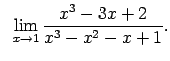 |
VIII.2.Atrast robežas.
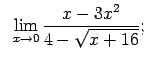 |
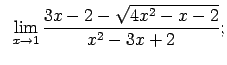 |
|||
![$\displaystyle \;\;\lim\limits_{x\rightarrow 1}\frac{\sqrt[3]{x-2}-\sqrt[3]{1-x+x^2}}{x^2-1};$](img1302.gif) |
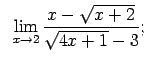 |
|||
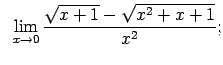 |
![$\displaystyle \;\;\lim\limits_{x\rightarrow 0}\frac{\sqrt[3]{1+x^2}-1}{x^2};$](img1305.gif) |
|||
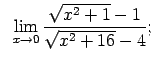 |
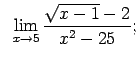 |
|||
![$\displaystyle \;\;\lim\limits_{x\rightarrow 0}\frac{\sqrt[3]{1+x}-\sqrt[3]{1-x}}{x};$](img1308.gif) |
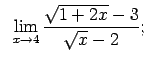 |
|||
![$\displaystyle \;\;\lim\limits_{x\rightarrow -8}\frac{\sqrt{1-x}-3}{2+\sqrt[3]{x}};$](img1310.gif) |
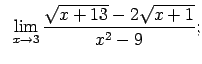 |
|||
![$\displaystyle \;\;\lim\limits_{x\rightarrow 16}\frac{\sqrt[4]{x}-2}{\sqrt{x}-4};$](img1312.gif) |
![$\displaystyle \;\;\lim\limits_{x\rightarrow -2}\frac{\sqrt[3]{x-6}+2}{x^3+8};$](img1313.gif) |
|||
![$\displaystyle \;\;\lim\limits_{x\rightarrow 8}\frac{\sqrt{9+2x}-5}{\sqrt[3]{x}-2};$](img1314.gif) |
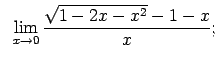 |
|||
![$\displaystyle \;\;\lim\limits_{x\rightarrow 0}\frac{\sqrt[3]{8+3x-x^2}-2}{x+x^2};$](img1316.gif) |
![$\displaystyle \;\;\lim\limits_{x\rightarrow 0}\frac{\sqrt[3]{27+x}-\sqrt[3]{27-x}}{x+2\sqrt[3]{x^4}};$](img1317.gif) |
|||
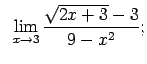 |
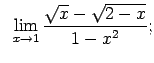 |
|||
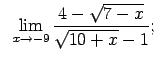 |
||||
![$\displaystyle \;\;\lim\limits_{x\rightarrow 1}\frac{\sqrt[3]{x}-1}{2-\sqrt{x+3}};$](img1322.gif) |
![$\displaystyle \;\;\lim\limits_{x\rightarrow -1}\frac{\sqrt{3x+7}-2}{1+\sqrt[3]{x}};$](img1323.gif) |
|||
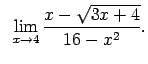 |
VIII.3.Atrast robežas.
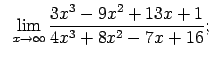 |
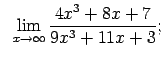 |
|||
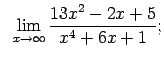 |
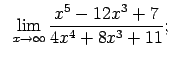 |
|||
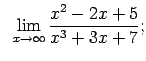 |
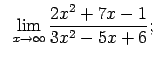 |
|||
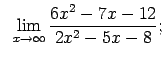 |
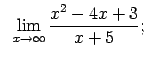 |
|||
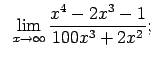 |
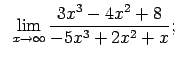 |
|||
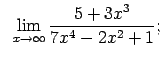 |
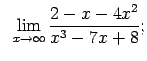 |
|||
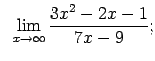 |
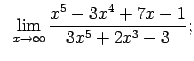 |
|||
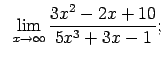 |
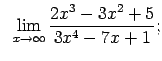 |
|||
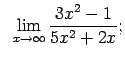 |
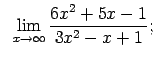 |
|||
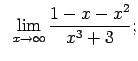 |
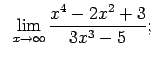 |
|||
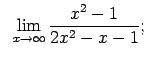 |
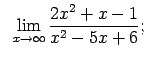 |
|||
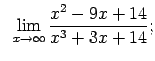 |
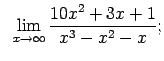 |
|||
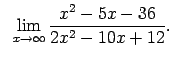 |
VIII.4.Atrast robežas.
VIII.5.Atrast robežas.
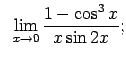 |
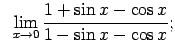 |
|||
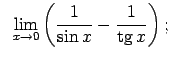 |
||||
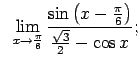 |
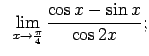 |
|||
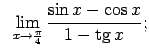 |
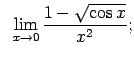 |
|||
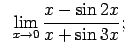 |
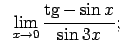 |
|||
 |
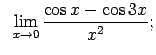 |
|||
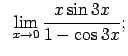 |
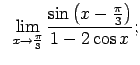 |
|||
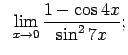 |
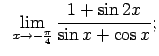 |
|||
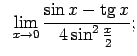 |
||||
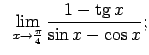 |
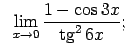 |
|||
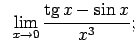 |
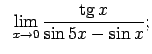 |
|||
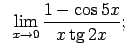 |
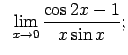 |
|||
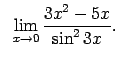 |
VIII.6.Atrast robežas.
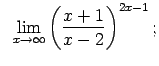 |
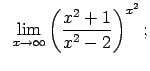 |
|||
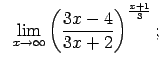 |
||||
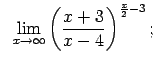 |
||||
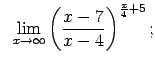 |
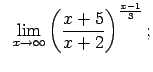 |
|||
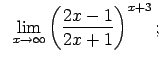 |
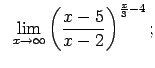 |
|||
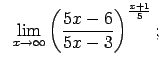 |
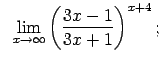 |
|||
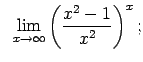 |
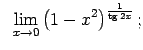 |
|||
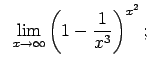 |
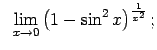 |
|||
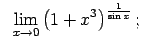 |
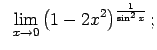 |
|||
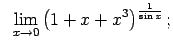 |
||||
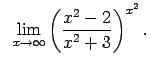 |
VIII.7.Atrast robežas.
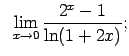 |
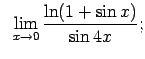 |
|||
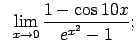 |
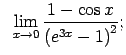 |
|||
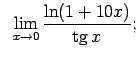 |
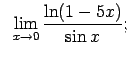 |
|||
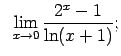 |
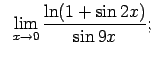 |
|||
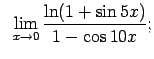 |
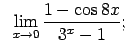 |
|||
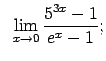 |
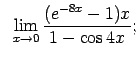 |
|||
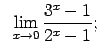 |
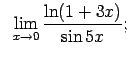 |
|||
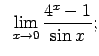 |
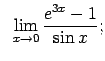 |
|||
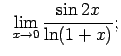 |
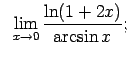 |
|||
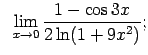 |
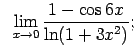 |
|||
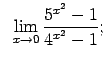 |
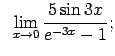 |
|||
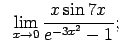 |
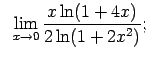 |
|||
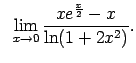 |
VIII.8.Atrast robežas.
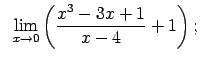 |
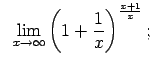 |
|||
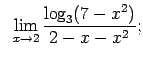 |
||||
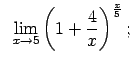 |
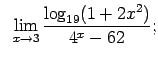 |
|||
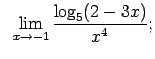 |
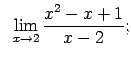 |
|||
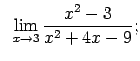 |
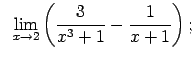 |
|||
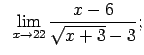 |
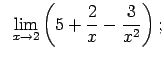 |
|||
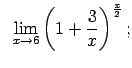 |
||||
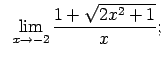 |
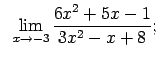 |
|||
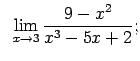 |
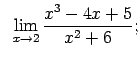 |
|||
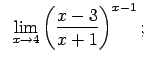 |
||||
![$\displaystyle \;\;\lim\limits_{x\rightarrow 6}\frac{\sqrt[3]{4x+3}-x\sqrt{x-2}}{2x-3};$](img1471.gif) |
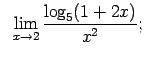 |
|||
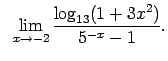 |
IX.Salīdzināt dotās bezgalīgi mazās funkcijas.
| kad |
||||||
| kad |
||||||
| kad |
||||||
| kad |
||||||
| kad |
||||||
| kad |
||||||
| kad |
||||||
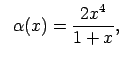 |
kad |
|||||
| kad |
||||||
| kad |
||||||
| kad |
||||||
| kad |
||||||
| kad |
||||||
| kad |
||||||
| kad |
||||||
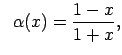 |
kad |
|||||
| kad |
||||||
| kad |
||||||
| kad |
||||||
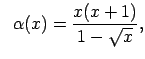 |
kad |
|||||
| kad |
||||||
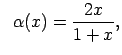 |
kad |
|||||
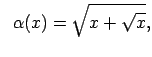 |
kad |
|||||
| kad |
||||||
| kad |
X.Pierādīt, ka dotās funkcijas ir nepārtrauktas punktā ![]() .
.
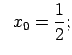 |
||||
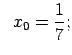 |
||||
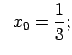 |
||||
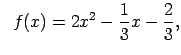 |
||||
XI.Atrast funkcijas pārtraukuma punktus un noteikt to veidu.
Konstruēt funkcijas shematisku grafiku.
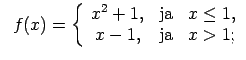 |
||
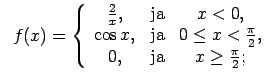 |
||
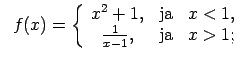 |
||
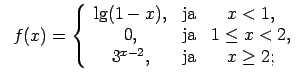 |
||
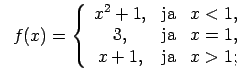 |
||
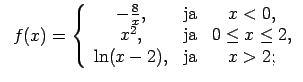 |
||
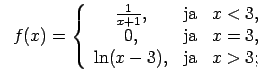 |
||
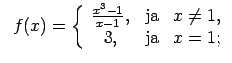 |
||
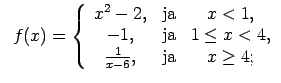 |
||
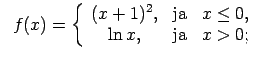 |
||
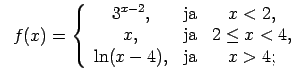 |
||
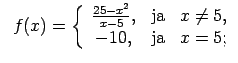 |
||
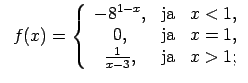 |
||
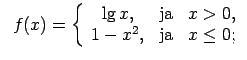 |
||
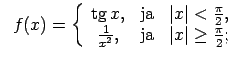 |
||
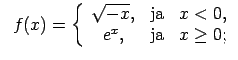 |
||
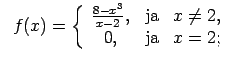 |
||
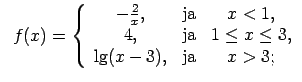 |
||
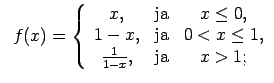 |
||
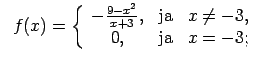 |
||
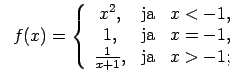 |
||
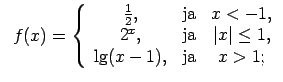 |
||
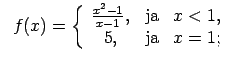 |
||
 |
||
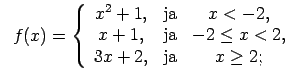 |
||
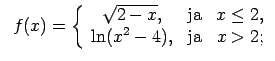 |
||
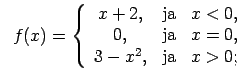 |
||
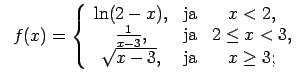 |
||
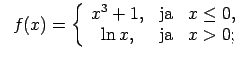 |
||
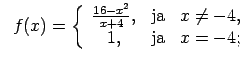 |
||
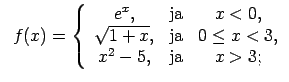 |
||
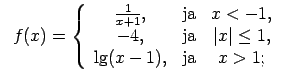 |
||
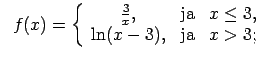 |
||
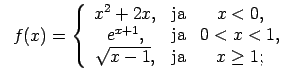 |
||
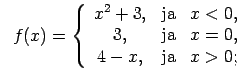 |
||
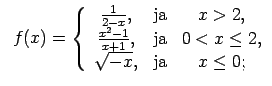 |
||
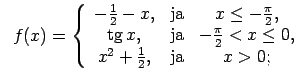 |
||
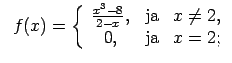 |
||
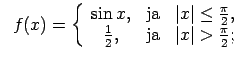 |
||
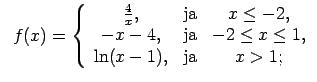 |
||
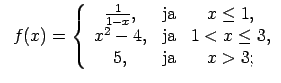 |
||
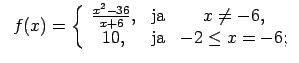 |
||
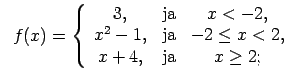 |
||
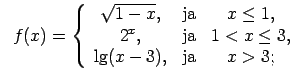 |
||
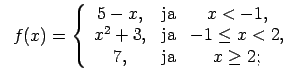 |
||
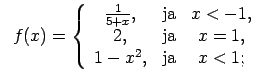 |
||
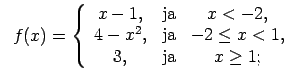 |
||
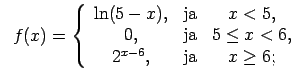 |
||
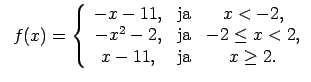 |
||
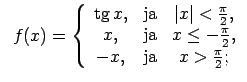 |