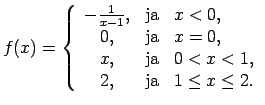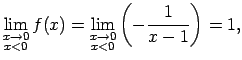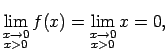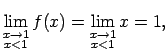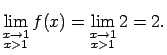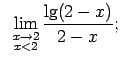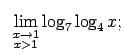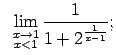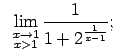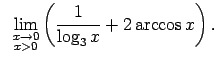Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 10.2. Funkcijas pārtraukuma punkti un to
Augstāk: 10. Vienpusējās robežas, to izskaitļošana. Funkcijas
Previous: 10. Vienpusējās robežas, to izskaitļošana. Funkcijas
-
10.1. definīcija.
- Punktu
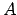 sauc par funkcijas
sauc par funkcijas  robežu punktā
robežu punktā
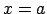 (
(
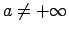 ) no labās puses, ja punkta
) no labās puses, ja punkta 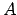 patvaļīgai apkārtnei
patvaļīgai apkārtnei 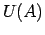 eksistē punkta
eksistē punkta 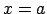 tāda apkārtne
tāda apkārtne
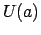 , ka visiem
, ka visiem 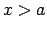 un
un 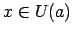 izpildās sakarība:
izpildās sakarība:
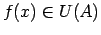 .
.
Apzīmē:
Analogi definē arī funkcijas robežu punktā no kreisās puses.
Acīmredzami, ja funkcijai  punktā
punktā 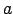 eksistē vienādas
vienpusējās robežas, tad šajā punktā tai eksistē robeža, kas ir
vienāda ar tās vienpusējām robežām. Ir spēkā arī apgrieztais
apgalvojums.
eksistē vienādas
vienpusējās robežas, tad šajā punktā tai eksistē robeža, kas ir
vienāda ar tās vienpusējām robežām. Ir spēkā arī apgrieztais
apgalvojums.
-
10.2. definīcija.
- Funkciju
 sauc par nepārtrauktu punktā
sauc par nepārtrauktu punktā 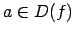 no kreisās puses (no labās puses), ja
no kreisās puses (no labās puses), ja
-
10.1. piem
 rs.
rs.
-

-
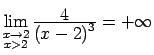 ,
,
jo 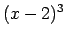 ir
pozitīva bezgalīgi maza funkcija, kad
ir
pozitīva bezgalīgi maza funkcija, kad
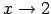 ;
jo
;
jo 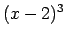 ir negatīva bezgalīgi maza funkcija, kad
ir negatīva bezgalīgi maza funkcija, kad
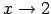 .
.
-
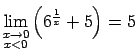 ,
,
jo
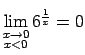 (ja
(ja
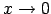 , bet
, bet
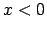 , tad
, tad
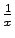 ir negatīva bezgalīgi liela funkcija);
jo
ir negatīva bezgalīgi liela funkcija);
jo
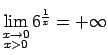 (ja
(ja
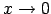 , bet
, bet
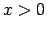 , tad
, tad
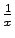 ir pozitīva bezgalīgi liela funkcija).
ir pozitīva bezgalīgi liela funkcija).
-
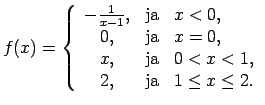
Auditorijā risināmie uzdevumi
- Atrast vienpusējās robežas funkcijām
- Atrast vienpusējās robežas punktos
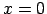 un
un
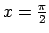 funkcijai
funkcijai



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 10.2. Funkcijas pārtraukuma punkti un to
Augstāk: 10. Vienpusējās robežas, to izskaitļošana. Funkcijas
Previous: 10. Vienpusējās robežas, to izskaitļošana. Funkcijas
2003-05-15
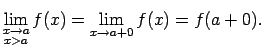
![]() punktā
punktā ![]() eksistē vienādas
vienpusējās robežas, tad šajā punktā tai eksistē robeža, kas ir
vienāda ar tās vienpusējām robežām. Ir spēkā arī apgrieztais
apgalvojums.
eksistē vienādas
vienpusējās robežas, tad šajā punktā tai eksistē robeža, kas ir
vienāda ar tās vienpusējām robežām. Ir spēkā arī apgrieztais
apgalvojums.
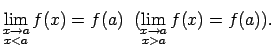
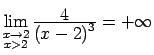 ,
,
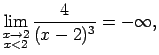
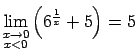 ,
,
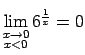 (ja
(ja
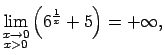
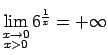 (ja
(ja