


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3. Reālā mainīgā reālu funkciju klasifikācija
Augstāk: vallievads2ht
Previous: 1. Reālā skaitļa modulis
Par atbilstību sauc sakārtotu pāru 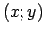 patvaļīgu kopu
patvaļīgu kopu
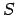 .
.
Pirmo elementu 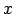 kopu sauc par atbilstības definīcijas
apgabalu
kopu sauc par atbilstības definīcijas
apgabalu 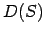 , bet otro elementu
, bet otro elementu 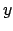 kopu - par atbilstības
vērtību apgabalu
kopu - par atbilstības
vērtību apgabalu 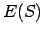 .
.
Atbilstību 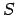 sauc par viennozīmīgu, ja katram
sauc par viennozīmīgu, ja katram 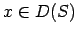 eksistē vienīgs
eksistē vienīgs 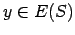 , ka
, ka
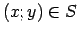 .
.
-
2.1. definīcija.
- Par funkciju sauc katru viennozīmīgu
atbilstību.
Ja  ir funkcija un
ir funkcija un 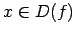 , tad
, tad 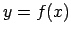 sauc par funkcijas
sauc par funkcijas
 vērtību punktā
vērtību punktā 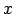 (skat.1).
(skat.1).
Divas funkcijas  un
un 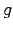 uzskata par vienādām, ja
uzskata par vienādām, ja
- tām ir vienādi definīcijas apgabali,
- katram
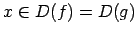 izpildās
izpildās 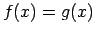 .
.
Par funkcijas  grafiku sauc kopu
grafiku sauc kopu
-
2.1. piem
 rs.
rs.
-
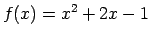 .
.
Atrast 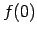 ,
, 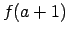 ,
,
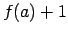 ,
,
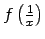 ,
,
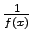 ,
,
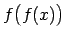 .
.
Ievietojot argumenta 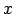 vietā 0, iegūst
Analogi
vietā 0, iegūst
Analogi
Lai atrastu
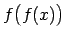 , argumenta
, argumenta 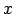 vietā ievieto
vietā ievieto
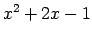 .
.
-
2.2. piem
 rs.
rs.
-
Atrast
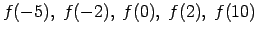 .
.
Funkcija ir definēta ar
3 formulām visiem
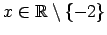 .
.
Tā kā
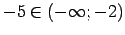 , tad
, tad
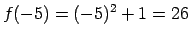 .
.
Skaitlis
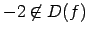 , t.i., funkcija šajā
punktā nav definēta, un funkcijas vērtība punktā
, t.i., funkcija šajā
punktā nav definēta, un funkcijas vērtība punktā 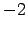 neeksistē.
neeksistē.
Skaitlis
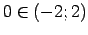 , tāpēc
, tāpēc
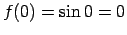 .
.
Skaitlis
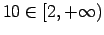 , tāpēc
, tāpēc
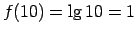 .
.
-
2.3. piem
 rs.
rs.
- Noskaidrot, vai dotās funkcijas ir vienādas.
-
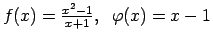 ,
,
-
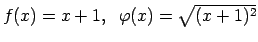 ,
,
-
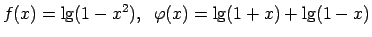 .
.
-
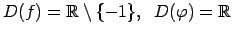 .
.
Tā kā
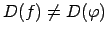 , tad dotās funkcijas nav
vienādas.
, tad dotās funkcijas nav
vienādas.
-
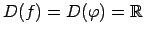 ,
,
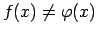 visiem
visiem
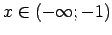 , piemēram,
, piemēram,
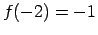 ,
,
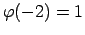 . Tātad dotās funkcijas nav
vienādas.
. Tātad dotās funkcijas nav
vienādas.
- Nosaka funkciju definīcijas apgabalus.
Tātad
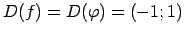 .
.
Visiem
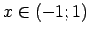 ir spēkā
Tātad dotās funkcijas ir vienādas.
ir spēkā
Tātad dotās funkcijas ir vienādas.
Auditorijā risināmie uzdevumi
-
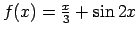 .
Atrast
.
Atrast
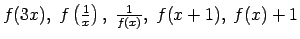 .
.
-
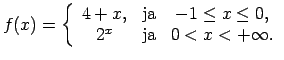
Atrast
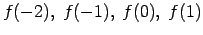 .
.
-
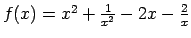 .
Parādīt, ka
.
Parādīt, ka
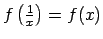 .
.
-
![$ \varphi(t)=\sqrt[3]{1-t^3}$](img223.gif) . Parādīt, ka
. Parādīt, ka
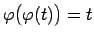 .
.
- Noteikt, kuras no dotajām funkcijām ir vienādas.
Mājas darba uzdevumi
-
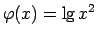 . Aprēķināt
. Aprēķināt
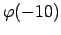 ,
,
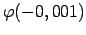 ,
,
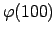 .
.
-
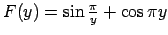 . Aprēķināt
. Aprēķināt 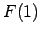 ,
,
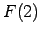 ,
, 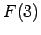 ,
, 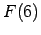 .
.
-
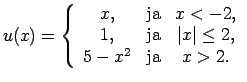
Atrast 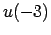 ,
, 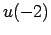 ,
, 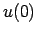 ,
, 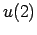 ,
, 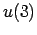 .
.
-
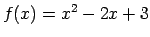 . Atrisināt vienādojumus.
. Atrisināt vienādojumus.
-
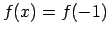 ,
,
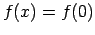 ,
,
-
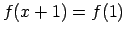 .
.
- Noteikt, kuras no dotajām funkcijām ir vienādas.
Definīcijas apgabala noteikšana analītiski definētām
funkcijām
Visbiežāk funkciju uzdod analītiski, t.i., ar formulu. Tādā
gadījumā funkcijas definīcijas apgabalu īpaši nenorāda. Ar
definīcijas apgabalu saprot tās argumenta vērtības, ar kurām
formulai ir jēga. Piemēram,
-
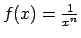 ,
,
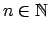 , tad
, tad 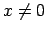 jeb
jeb
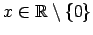 ;
;
-
![$ f(x)=\sqrt[m]{x}$](img272.gif) ,
, 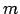 ir pāra skaitlis, tad
ir pāra skaitlis, tad 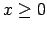 jeb
jeb
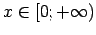 ;
;
-
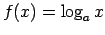 , tad
, tad 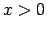 jeb
jeb
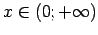 ;
;
-
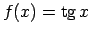 , tad
, tad
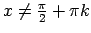 jeb
jeb
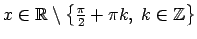 ;
;
-
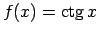 , tad
, tad
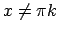 jeb
jeb
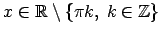 ;
;
-
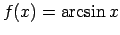 , tad
, tad 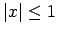 jeb
jeb
![$ x\in[-1;1]$](img287.gif) ;
;
-
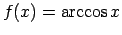 , tad
, tad 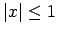 jeb
jeb
![$ x\in[-1;1]$](img287.gif) .
.
-
2.4. piem
 rs.
rs.
- Noteikt funkcijas
definīcijas apgabalu.
Dotās funkcijas definīcijas apgabals ir abu saskaitāmo
definīcijas apgabalu kopējā daļa.
Atbilde.
![$ x\in\left[\frac{3}{5};\frac{7}{3}\right]$](img295.gif) .
.
-
2.5. piem
 rs.
rs.
- Noteikt funkcijas
definīcijas apgabalu.
Šoreiz
Atbilde.
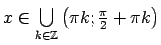 .
.
-
2.6. piem
 rs.
rs.
- Noteikt funkcijas
definīcijas apgabalu.
Šoreiz jāatrisina nevienādību sistēma:
Atbilde.
![$ x\in\left(\frac{1}{2};1\right]$](img305.gif) .
.
Auditorijā risināmie uzdevumi
Noteikt funkciju definīcijas apgabalus.
-
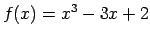 ;
;
-
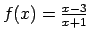 ;
;
-
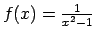 ;
;
-
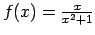 ;
;
-
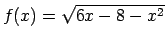 ;
;
-
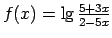 ;
;
-
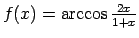 ;
;
-
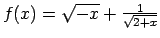 ;
;
-
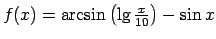 ;
;
-
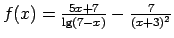 ;
;
-
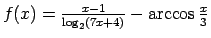 ;
;
-
![$ f(x)=\sqrt[3]{\lg\frac{3x-7}{5}}+3^{\frac{x}{5-x}}$](img317.gif) ;
;
-
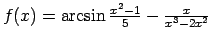 ;
;
-
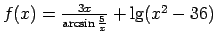 ;
;
-
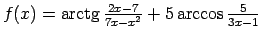 .
.
Mājas darba uzdevumi
Noteikt funkciju definīcijas apgabalus.
-
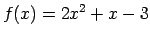 ;
;
-
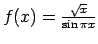 ;
;
-
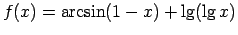 ;
;
-
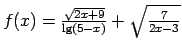 ;
;
-
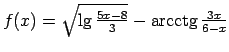 ;
;
-
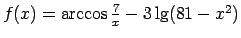 ;
;
-
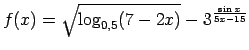 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3. Reālā mainīgā reālu funkciju klasifikācija
Augstāk: vallievads2ht
Previous: 1. Reālā skaitļa modulis
2003-05-15
![]() patvaļīgu kopu
patvaļīgu kopu
![]() .
.
![]() ir funkcija un
ir funkcija un ![]() , tad
, tad ![]() sauc par funkcijas
sauc par funkcijas
![]() vērtību punktā
vērtību punktā ![]() (skat.1).
(skat.1).
![]() grafiku sauc kopu
grafiku sauc kopu
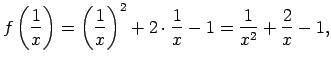
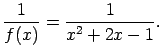
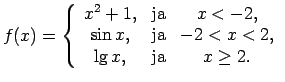
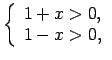
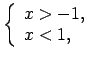
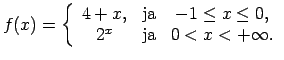
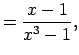
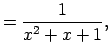
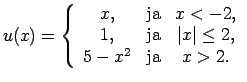
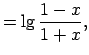
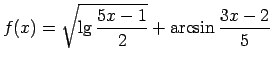
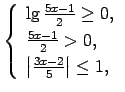
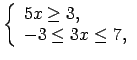
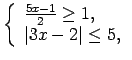
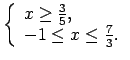
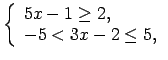
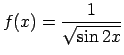
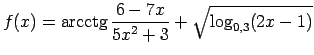
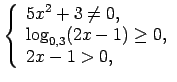
![$ f(x)=\sqrt[3]{\lg\frac{3x-7}{5}}+3^{\frac{x}{5-x}}$](img317.gif) ;
;
 ;
;
 ;
;
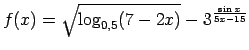 .
.