Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2. Funkcijas jēdziens. Vienādas funkcijas. Funkcijas,
Augstāk: vallievads2ht
Previous: vallievads2ht
-
1.1. definīcija.
- Par reālā skaitļa
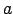 moduli (absolūto
vērtību) sauc
moduli (absolūto
vērtību) sauc
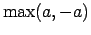 un apzīmē
un apzīmē 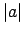 .
.
Tādējādi
Moduļa īpašības.
-
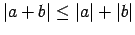 ;
;
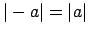 ;
;
-
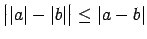 ;
;
-
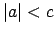 tad un tikai tad, ja
tad un tikai tad, ja 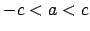 ;
;
-
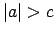 tad un tikai tad, ja
tad un tikai tad, ja 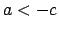 vai
vai 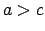 ;
;
-
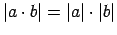 ;
;
-
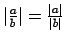 , ja
, ja 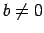 .
.
Risinot vienādojumus un nevienādības, kas satur moduli, ir
izdevīgi lietot intervālu metodi, kuras pamatā ir
nepārtrauktu funkciju īpašība: ja funkcija  intervālā
intervālā
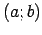 ir nepārtraukta un nevienā šī intervāla punktā tās vērtība
nav 0, tad visos intervāla punktos funkcijas vērtības ir vai nu
tikai pozitīvas, vai arī tikai negatīvas. Ja pieņem, ka funkcija
ir nepārtraukta un nevienā šī intervāla punktā tās vērtība
nav 0, tad visos intervāla punktos funkcijas vērtības ir vai nu
tikai pozitīvas, vai arī tikai negatīvas. Ja pieņem, ka funkcija
 ir nepārtraukta intervālā
ir nepārtraukta intervālā 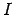 un to intervāla punktu
skaits, kuros šīs funkcijas vērtības vienādas ar nulli, ir galīgs,
tad šie punkti sadala intervālu
un to intervāla punktu
skaits, kuros šīs funkcijas vērtības vienādas ar nulli, ir galīgs,
tad šie punkti sadala intervālu 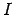 apakšintervālos, pie
tam katra apakšintervāla visos punktos funkcijas
apakšintervālos, pie
tam katra apakšintervāla visos punktos funkcijas  vērtības ir vai nu pozitīvas, vai arī negatīvas. Lai noteiktu
funkcijas vērtību zīmi kādā apakšintervālā, pietiek
aprēķināt funkcijas vērtību brīvi izraudzītā dotā
apakšintervāla punktā.
vērtības ir vai nu pozitīvas, vai arī negatīvas. Lai noteiktu
funkcijas vērtību zīmi kādā apakšintervālā, pietiek
aprēķināt funkcijas vērtību brīvi izraudzītā dotā
apakšintervāla punktā.
1.1. piem rs.
rs.
- Konstruēt funkcijas
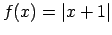 grafiku.
grafiku.
Šo uzdevumu var atrisināt ar vairākiem paņēmieniem.
1. paņēmiens.
Pārveido šīs funkcijas analītisko izskatu, izmantojot moduļa
definīciju. Punkts 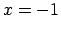 sadala koordinātu taisni divos
intervālos. Katrā no šiem intervāliem (1.1. zīm.) nosaka
funkcijas izskatu.
sadala koordinātu taisni divos
intervālos. Katrā no šiem intervāliem (1.1. zīm.) nosaka
funkcijas izskatu.
Intervālā
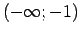 ir spēkā
ir spēkā 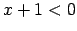 , tāpēc
, tāpēc
un
Intervālā
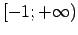 ir spēkā
ir spēkā 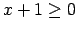 , tāpēc
Tātad doto funkciju var uzrakstīt šādi:
, tāpēc
Tātad doto funkciju var uzrakstīt šādi:
Konstruē šīs funkcijas grafiku (1.2. zīm).
2. paņēmiens.
Konstruē funkcijas 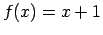 grafiku un grafika to daļu, kas
atrodas zem
grafiku un grafika to daļu, kas
atrodas zem 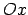 ass, attēlo simetriski attiecībā pret
ass, attēlo simetriski attiecībā pret 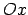 asi
(1.3. zīm.).
asi
(1.3. zīm.).
3. paņēmiens.
Funkcijas
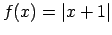 grafiku var iegūt no funkcijas
grafiku var iegūt no funkcijas 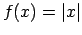 grafika, veicot paralēlo pārnesi par vienu vienību pa kreisi
(1.4. zīm.).
grafika, veicot paralēlo pārnesi par vienu vienību pa kreisi
(1.4. zīm.).
1.2. piem rs.
rs.
- Konstruēt funkcijas
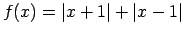 grafiku.
grafiku.
Lietojot intervālu metodi un moduļa definīciju, pārveido dotās
funkcijas analītisko izskatu.
- Ja
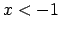 , tad
, tad 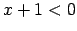 un
un 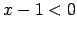 , tāpēc
, tāpēc
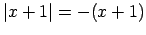 un
un
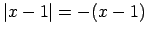 .
.
Tātad
- Ja
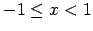 , tad
, tad 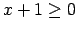 un
un 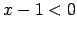 , tāpēc
, tāpēc 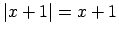 un
un
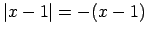 .
.
Tātad
- Ja
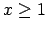 , tad
, tad 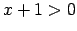 un
un 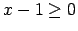 , tāpēc
, tāpēc 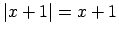 un
un
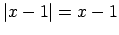 .
.
Tātad
Ņemot vērā funkcijas analītisko izskatu katrā no minētajiem
intervāliem, var rakstīt:
Konstruē šīs funkcijas grafiku (1.6. zīm.).
1.3. piem rs.
rs.
- Atrisināt vienādojumu
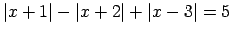 .
.
Punkti 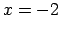 ,
, 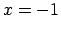 un
un 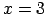 koordinātu taisni sadala četros
intervālos (1.7. zīm.). Katrā no šiem intervāliem katra no
izteiksmēm, kas atrodas zem moduļa zīmes, saglabā savu zīmi.
koordinātu taisni sadala četros
intervālos (1.7. zīm.). Katrā no šiem intervāliem katra no
izteiksmēm, kas atrodas zem moduļa zīmes, saglabā savu zīmi.
Lietojot moduļa definīciju, katrā no šiem intervāliem doto
vienādojumu var pārrakstīt šādi:
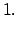 |
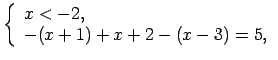 |
|
| |
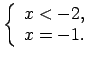 |
|
| |
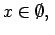 jo jo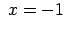 nepieder šim intervālam nepieder šim intervālam |
|
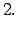 |
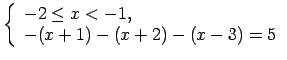 |
|
| |
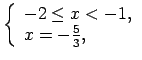 |
|
| |
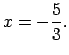 |
|
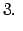 |
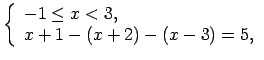 |
|
| |
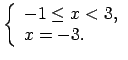 |
|
| |
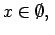 jo jo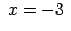 nepieder šim intervālam nepieder šim intervālam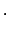 |
|
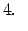 |
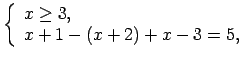 |
|
| |
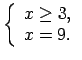 |
|
| |
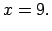 |
|
| |
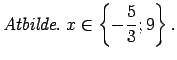 |
|
-
1.4. piem
 rs.
rs.
- Atrisināt nevienādību
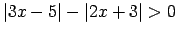 .
.
Punkti
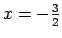 un
un
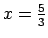 sadala koordinātu
taisni trīs intervālos (1.8. zīm.).
sadala koordinātu
taisni trīs intervālos (1.8. zīm.).
Pārraksta doto nevienādību katrā no šiem intervāliem.
Lai uzrakstītu atbildi, apvieno iegūtos rezultātus uz koordinātu
taisnes (1.9. zīm.).
Atbilde.
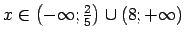 .
.
-
1.5. piem
 rs.
rs.
- Atrisināt nevienādību
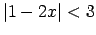 .
.
Doto nevienādību var atrisināt, izmantojot moduļa 4. īpašību.
Atbilde.
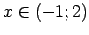 .
.
-
1.6. piem
 rs.
rs.
- Atrisināt nevienādību
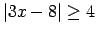 .
.
Doto nevienādību var atrisināt, izmantojot moduļa 5. īpašību.
Atbilde.
![$ x\in\left(-\infty;\frac{4}{3}\right]\cup[4;+\infty)$](img118.gif) .
.
-
1.7. piem
 rs.
rs.
- Atrisināt vienādojumu
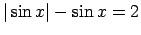 .
.
- Ja
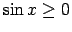 , tad
, tad
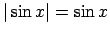 , tāpēc
, tāpēc
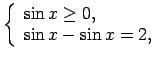
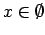 .
.
- Ja
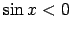 , tad
, tad
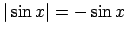 , tāpēc
, tāpēc
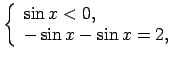
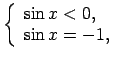
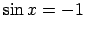 .
.
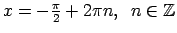 .
.
Atbilde.
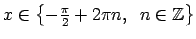 .
.
Auditorijā risināmie uzdevumi
- Konstruēt grafikus funkcijām
-
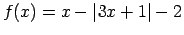 ,
,
-
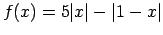 ,
,
-
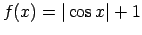 .
.
- Atrisināt vienādojumus
-
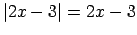 ,
,
-
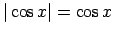 ,
,
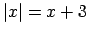 ,
,
-
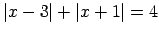 ,
,
-
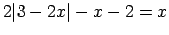 .
.
- Atrisināt nevienādības
-
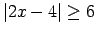 ,
,
-
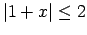 ,
,
-
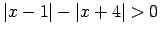 ,
,
-
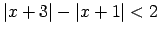 ,
,
-
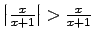 ,
,
-
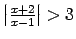 ,
,
-
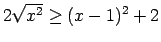 ,
,
-
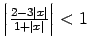 .
.
Mājas darba uzdevumi
- Konstruēt grafikus funkcijām
-
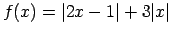 ,
,
-
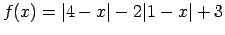 ,
,
-
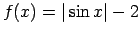 .
.
- Atrisināt vienādojumus
-
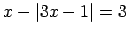 ,
,
-
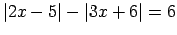 ,
,
-
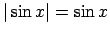 ,
,
-
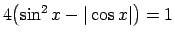 .
.
- Atrisināt nevienādības
-
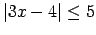 ,
,
-
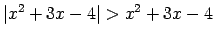 ,
,
-
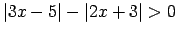 ,
,
-
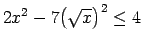 ,
,
-
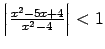 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2. Funkcijas jēdziens. Vienādas funkcijas. Funkcijas,
Augstāk: vallievads2ht
Previous: vallievads2ht
2003-05-15
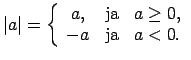
![]() intervālā
intervālā
![]() ir nepārtraukta un nevienā šī intervāla punktā tās vērtība
nav 0, tad visos intervāla punktos funkcijas vērtības ir vai nu
tikai pozitīvas, vai arī tikai negatīvas. Ja pieņem, ka funkcija
ir nepārtraukta un nevienā šī intervāla punktā tās vērtība
nav 0, tad visos intervāla punktos funkcijas vērtības ir vai nu
tikai pozitīvas, vai arī tikai negatīvas. Ja pieņem, ka funkcija
![]() ir nepārtraukta intervālā
ir nepārtraukta intervālā ![]() un to intervāla punktu
skaits, kuros šīs funkcijas vērtības vienādas ar nulli, ir galīgs,
tad šie punkti sadala intervālu
un to intervāla punktu
skaits, kuros šīs funkcijas vērtības vienādas ar nulli, ir galīgs,
tad šie punkti sadala intervālu ![]() apakšintervālos, pie
tam katra apakšintervāla visos punktos funkcijas
apakšintervālos, pie
tam katra apakšintervāla visos punktos funkcijas ![]() vērtības ir vai nu pozitīvas, vai arī negatīvas. Lai noteiktu
funkcijas vērtību zīmi kādā apakšintervālā, pietiek
aprēķināt funkcijas vērtību brīvi izraudzītā dotā
apakšintervāla punktā.
vērtības ir vai nu pozitīvas, vai arī negatīvas. Lai noteiktu
funkcijas vērtību zīmi kādā apakšintervālā, pietiek
aprēķināt funkcijas vērtību brīvi izraudzītā dotā
apakšintervāla punktā.
![]() rs.
rs. ![]() ir spēkā
ir spēkā ![]() , tāpēc
, tāpēc
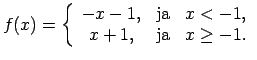
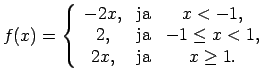
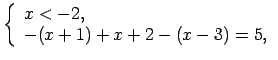
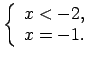
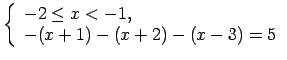
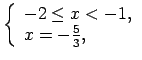
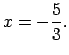
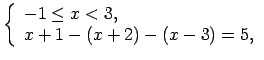
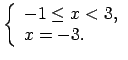
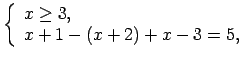
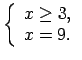
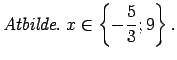
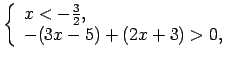
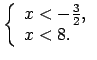
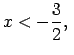 tātad
tātad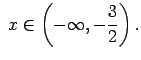
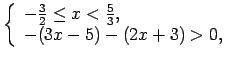
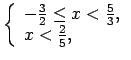
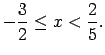
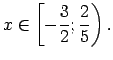
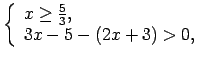
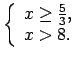
![]() .
.
![$\displaystyle \in\left(-\infty;\frac{4}{3}\right].$](img117.gif)