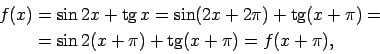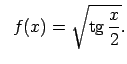Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4. Apvērstā (inversā) funkcija
Augstāk: 3. Reālā mainīgā reālu funkciju klasifikācija
Previous: 3.1. Pāra un nepāra funkcijas
Apskata funkcijas, kuru definīcijas apgabali apmierina šādu
nosacījumu: visiem 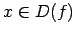 arī
arī
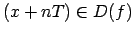 (
(
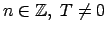 ).
).
-
3.3. definīcija.
- Funkciju
 sauc par periodisku funkciju ar
periodu
sauc par periodisku funkciju ar
periodu 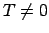 , ja katram
, ja katram 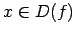 ir pareiza vienādība
ir pareiza vienādība
Par funkcijas periodiem der arī skaitļi 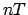 , kur
, kur
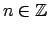 . Vismazāko no šiem skaitļiem sauc par
mazāko pozitīvo periodu2.
. Vismazāko no šiem skaitļiem sauc par
mazāko pozitīvo periodu2.
-
3.2. piem
 rs.
rs.
- Pierādīt, ka
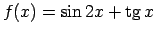 ir periodiska
funkcija un atrast tās periodu.
ir periodiska
funkcija un atrast tās periodu.
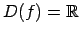 .
.
Tā kā sinusa periods ir 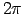 un tangensa periods ir
un tangensa periods ir 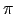 ,
tad
,
tad
tātad dotā funkcija ir periodiska, un tās periods 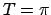 .
.
-
3.3. piem
 rs.
rs.
- Pierādīt, ka funkcija
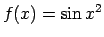 nav
periodiska.
nav
periodiska.
Pieņem, ka eksistē tāds skaitlis 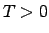 , ka visiem
, ka visiem
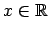 ir spēkā vienādība
Izvēloties
ir spēkā vienādība
Izvēloties 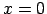 , iegūst:
, iegūst:
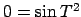 . Izsakot
. Izsakot 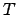 un
ievietojot šo
un
ievietojot šo 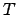 vērtību vienādībā (*), nonāk pie pretrunas.
Tās nozīmē, ka funkcija
vērtību vienādībā (*), nonāk pie pretrunas.
Tās nozīmē, ka funkcija
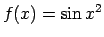 nav
periodiska3.
nav
periodiska3.
Auditorijā risināmie uzdevumi
Noteikt, vai funkcijas ir periodiskas, periodiskām funkcijām
noteikt to periodus.
Mājas darba uzdevumi



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4. Apvērstā (inversā) funkcija
Augstāk: 3. Reālā mainīgā reālu funkciju klasifikācija
Previous: 3.1. Pāra un nepāra funkcijas
2003-05-15
![]() arī
arī
![]() (
(
![]() ).
).
![]() , kur
, kur
![]() . Vismazāko no šiem skaitļiem sauc par
mazāko pozitīvo periodu2.
. Vismazāko no šiem skaitļiem sauc par
mazāko pozitīvo periodu2.