Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.2. Periodiskas funkcijas
Augstāk: 3. Reālā mainīgā reālu funkciju klasifikācija
Previous: 3. Reālā mainīgā reālu funkciju klasifikācija
Apskata funkcijas, kuru definīcijas apgabali ir simetriski
attiecībā pret koordinātu sākuma punktu, t.i., funkcijas,
kurām reizē ar 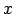 definīcijas apgabalam pieder arī
definīcijas apgabalam pieder arī 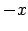 .
.
-
3.1. definīcija.
- Funkciju
 sauc par pāra funkciju, ja
sauc par pāra funkciju, ja
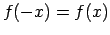 visiem
visiem 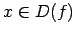 .
.
-
3.2. definīcija.
- Funkciju
 sauc par nepāra funkciju, ja
sauc par nepāra funkciju, ja
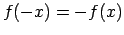 visiem
visiem 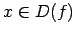 .
.
No šīm definīcijām seko, ka pāra funkcijas grafiks ir simetrisks
attiecībā pret ordinātu asi, bet nepāra funkcijas grafiks ir
simetrisks attiecībā pret koordinātu sākuma punktu.
-
3.1. piem
 rs.
rs.
- Noteikt, vai dotās funkcijas ir pāra vai nepāra
funkcijas.
-
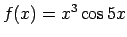 ,
,
-
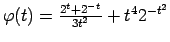 ,
,
-
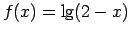 .
.
-
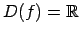 , tātad simetrisks attiecībā pret
koordinātu sākuma punktu.
, tātad simetrisks attiecībā pret
koordinātu sākuma punktu.
Atrod
Atbilde. Dotā funkcija ir nepāra funkcija.
-
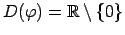 - simetriska
attiecībā pret koordinātu sākuma punktu kopa.
Atbilde. Dotā funkcija ir pāra funkcija.
- simetriska
attiecībā pret koordinātu sākuma punktu kopa.
Atbilde. Dotā funkcija ir pāra funkcija.
-
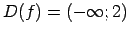 - nav simetrisks attiecībā pret
koordinātu sākuma punktu, tāpēc dotā funkcija nevar būt ne
pāra, ne nepāra funkcija.
- nav simetrisks attiecībā pret
koordinātu sākuma punktu, tāpēc dotā funkcija nevar būt ne
pāra, ne nepāra funkcija.
Auditorijā risināmie uzdevumi
Noteikt, vai dotās funkcijas ir pāra vai nepāra funkcijas.
-
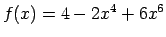 .
.
-
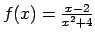 .
.
-
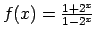 .
.
-
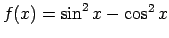 ;
;
-
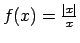 .
.
-
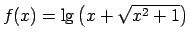 .
.
- Funkcija
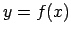 ir definēta slēgtā intervālā
ir definēta slēgtā intervālā ![$ [-a;a]$](img345.gif) .
3.1. zīmējumā attēlots šīs funkcijas grafiks intervālā
.
3.1. zīmējumā attēlots šīs funkcijas grafiks intervālā ![$ [0;a]$](img346.gif) .
Turpināt funkcijas grafiku intervālā
.
Turpināt funkcijas grafiku intervālā 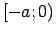 , ja zināms, ka
, ja zināms, ka
 - pāra funkcija,
- pāra funkcija,
 - nepāra funkcija.
- nepāra funkcija.
- Pierādīt, ka divu pāra funkciju reizinājums ir pāra funkcija.
Mājas darba uzdevumi
- Noteikt, vai dotās funkcijas ir pāra vai nepāra funkcijas.
-
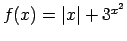 ;
;
-
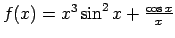 ;
;
-
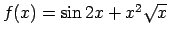 ;
;
-
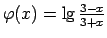 ;
;
-
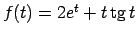 .
.
- Pierādīt, ka divu pāra funkciju summa ir pāra funkcija.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3.2. Periodiskas funkcijas
Augstāk: 3. Reālā mainīgā reālu funkciju klasifikācija
Previous: 3. Reālā mainīgā reālu funkciju klasifikācija
2003-05-15
![]() definīcijas apgabalam pieder arī
definīcijas apgabalam pieder arī ![]() .
.