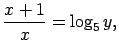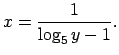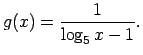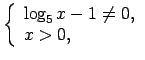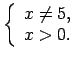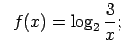Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 5. Konverģentas skaitļu virknes
Augstāk: vallievads2ht
Previous: 3.2. Periodiskas funkcijas
-
4.1. definīcija.
- Funkciju
 , kas iegūst katru savu vērtību tikai
vienā definīcijas apgabala punktā, sauc par apvēršamu
funkciju.
, kas iegūst katru savu vērtību tikai
vienā definīcijas apgabala punktā, sauc par apvēršamu
funkciju.
Piemēram, intervālā 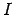 stingri monotona funkcija ir apvēršama
šajā intervālā.
stingri monotona funkcija ir apvēršama
šajā intervālā.
-
4.2. definīcija.
- Funkciju
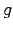 , kas apvēršamās funkcijas
, kas apvēršamās funkcijas  vērtību apgabala katrā punktā
vērtību apgabala katrā punktā 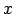 iegūst tādu vērtību
iegūst tādu vērtību 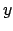 , ka
, ka
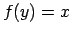 , sauc par funkcijas
, sauc par funkcijas  apvērsto (inverso) funkciju.
apvērsto (inverso) funkciju.
Tātad apvērsto funkciju 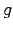 var definēt tikai apvēršamai funkcijai
var definēt tikai apvēršamai funkcijai
 , pie tam
, pie tam 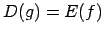 un
un 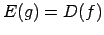 .
.
Apvēršamai funkcijai  eksistē vienīgā apvērstā funkcija
eksistē vienīgā apvērstā funkcija 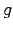 , un
tās grafiks ir simetrisks funkcijas
, un
tās grafiks ir simetrisks funkcijas  grafikam attiecībā pret
taisni
grafikam attiecībā pret
taisni 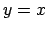 .
.
Lai funkcijai 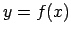 ,
, 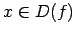 , atrastu apvērsto funkciju,
, atrastu apvērsto funkciju,
- pārliecinās par to, ka funkcija
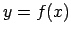 ir apvēršama
tās definīcijas apgabalā4,
ir apvēršama
tās definīcijas apgabalā4,
- atrisina vienādojumu
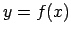 attiecībā pret
attiecībā pret
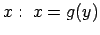 ,
,
- argumentu apzīmē ar
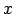 un funkcijas
vērtību - ar
un funkcijas
vērtību - ar
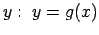 .
.
-
4.1. piem
 rs.
rs.
- Atrast funkcijas
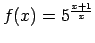 apvērsto funkciju un noteikt tās definīcijas apgabalu.
apvērsto funkciju un noteikt tās definīcijas apgabalu.
Dotā funkcija ir apvēršama, tās definīcijas apgabals
Lai atrastu funkcijas apvērsto funkciju, jāatrisina
vienādojums
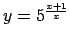 attiecībā pret
attiecībā pret 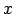 .
Argumentu apzīmējot ar
.
Argumentu apzīmējot ar 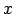 , iegūst
Atrod
, iegūst
Atrod 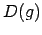 :
:
Tātad
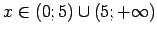 .
.
-
4.2. piem
 rs.
rs.
- Atrast funkcijas
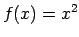 apvērsto funkciju,
noteikt tās definīcijas apgabalu un konstruēt dotās un
apvērstās funkcijas grafiku.
apvērsto funkciju,
noteikt tās definīcijas apgabalu un konstruēt dotās un
apvērstās funkcijas grafiku.
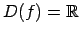 . Dotā funkcija nav apvēršama definīcijas
apgabalā, tāpēc jāizvēlas funkcijas sašaurinājums, piemēram,
uz intervālu
. Dotā funkcija nav apvēršama definīcijas
apgabalā, tāpēc jāizvēlas funkcijas sašaurinājums, piemēram,
uz intervālu
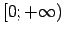 .
.
Šajā intervālā funkcija ir augoša, tātad tā ir apvēršama.
No vienādojuma 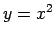 atrodam, ka
atrodam, ka
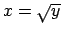 (pirms saknes jāņem
(pirms saknes jāņem 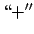 zīme, jo
zīme, jo
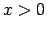 ) ir dotās funkcijas apvērstā funkcija.
) ir dotās funkcijas apvērstā funkcija.
Visbeidzot,
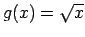 ,
,
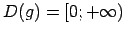 .
.
Auditorijā risināmie uzdevumi
Atrast dotajām funkcijām apvērstās funkcijas un noteikt to
definīcijas apgabalus. 1. un
4. piemērā konstruēt dotās un apvērstās
funkcijas grafiku.
-
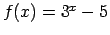 ;
;
-
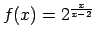 ;
;
-
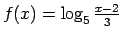 ;
;
-
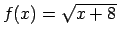 ;
;
-
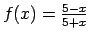 ;
;
-
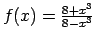 ;
;
-
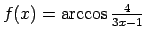 ;
;
-
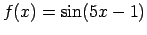 , ja
, ja
![$ x\in\left[-\frac{\pi}{10}+\frac{1}{5};\frac{\pi}{10}+\frac{1}{5}\right]$](img423.gif) ;
;
-
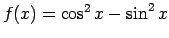 , ja
, ja
![$ x\in\left[0;\frac{\pi}{2}\right]$](img425.gif) .
.
Mājas darba uzdevumi



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 5. Konverģentas skaitļu virknes
Augstāk: vallievads2ht
Previous: 3.2. Periodiskas funkcijas
2003-05-15
![]() stingri monotona funkcija ir apvēršama
šajā intervālā.
stingri monotona funkcija ir apvēršama
šajā intervālā.
![]() var definēt tikai apvēršamai funkcijai
var definēt tikai apvēršamai funkcijai
![]() , pie tam
, pie tam ![]() un
un ![]() .
.