Raksta
![]() un saka, ka
virkne
un saka, ka
virkne ![]() konverģē uz skaitli
konverģē uz skaitli ![]() .
.
Atrisinot nevienādību
Tas nozīmē, ka visiem ![]()
![]() pieder punkta
pieder punkta ![]()
![]() - apkārtnei, t.i.,
- apkārtnei, t.i.,
![]() . Ārpus šīs apkārtnes atrodas tikai galīgs skaits
virknes locekļu.
. Ārpus šīs apkārtnes atrodas tikai galīgs skaits
virknes locekļu.
Virknes locekļus var attēlot kā koordinātu taisnes punktus (5.1. zīm.), var arī konstruēt virknes (kā funkcijas atsevišķa gadījuma) grafiku koordinātu plaknē. Šoreiz koordinātu plaknē iegūst izolētus punktus (5.2. zīm.).
Piemēram,
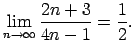
Pārveido starpību
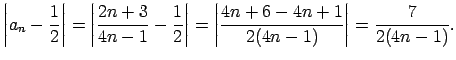
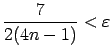
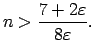
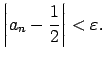
Piemēram, ja
![$\displaystyle N=\left[\frac{7+2\cdot 0,1}{8\cdot 0,1}\right]=\left[\frac{7,2}{0,8}\right]=9\/.$](img459.gif)
Dotās virknes robežas ģeometriskā interpretācija ir sniegta 5.2. zīm.
|
|
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
|
1,67 | 1 | 0,81 | 0,73 | 0,68 | 0,65 | 0,63 | 0,61 | 0,60 | 0,59 |
|
|
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|
|
0,58 | 0,57 | 0,57 | 0,56 | 0,56 | 0,56 | 0,55 | 0,55 | 0,55 | 0,54 |
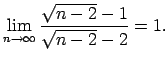
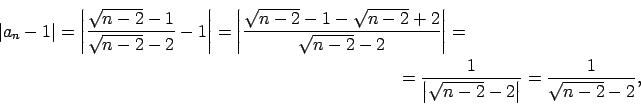
Atrisina nevienādību
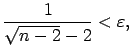 |
|
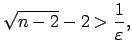 |
|
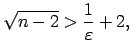 |
|
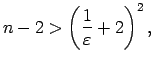 |
|
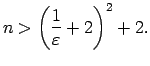 |
![$\displaystyle N=\max\Biggl\{\left[\left(\frac{1}{\varepsilon}+2\right)^2+2\right];6\Biggr\}\/,$](img471.gif)
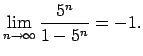
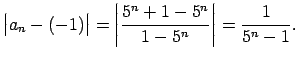
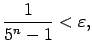 |
|
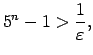 |
|
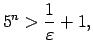 |
|
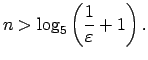 |
Auditorijā risināmie uzdevumi
Lietojot virknes robežas definīciju, pierādīt dotās vienādības.
Skaitlim
![]() atrast atbilstošo
atrast atbilstošo ![]() .
.
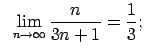 |
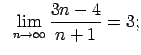 |
|||
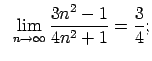 |
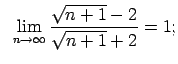 |
|||
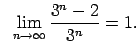 |
Mājas darba uzdevumi
Lietojot virknes robežas definīciju, pierādīt dotās vienādības.
Skaitlim
![]() atrast atbilstošo
atrast atbilstošo ![]() .
.
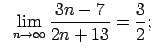 |
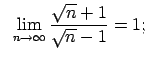 |
|||
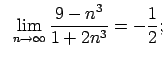 |
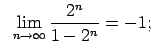 |
|||
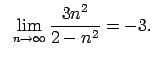 |