


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2.10. Uzdevumi
Augstāk: 1.2. Nosacītais ekstrēms
Iepriekšējais: 1.2.8. Uzdevumi
Vispirms atzīmēsim, ka, ja nosacītā ekstrēma problēmu var reducēt
uz brīvā ekstrēma meklēšanas problēmu (piemēram, izslēdzot
atkarīgos mainīgos), tad ir spēkā visi brīvā ekstrēma
pietiekamie nosacījumi.
-
1.6. piemērs.
- Aplūkosim nosacītā ekstrēma problēmu:
Acīmredzot, šī problēma ir ekvivalenta brīvā ekstrēma meklēšanas
problēmai:
Funkcijas 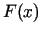 stacionārais punkts ir
stacionārais punkts ir
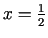 (vienādojuma
(vienādojuma
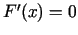 atrisinājums). Tā kā
atrisinājums). Tā kā
 , tad stacionārais punkts ir minimuma
punkts. Sākotnējās problēmās atrisinājums ir punkts
, tad stacionārais punkts ir minimuma
punkts. Sākotnējās problēmās atrisinājums ir punkts
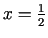 ,
,
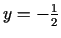 , kurā funkcija
, kurā funkcija 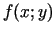 pieņem
minimālo vērtību.
pieņem
minimālo vērtību.
Ja nevar izteikt atkarīgos mainīgos ar neatkarīgiem, vai arī
iegūtie vienādojumi ir grūti atrisināmi, ir jāmeklē cita
pieeja.
Aplūkosim vispārīgu gadījumu (pēc
grāmatas [3]):
Pieņemsim, ka 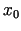 ir Lagranža funkcijas
ir Lagranža funkcijas
stacionārais punkts, bet
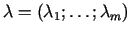 ir attiecīgais Lagranža
reizinātāju vektors. Stacionārā punkta raksturs ir atkarīgs no
funkcijas pieauguma
ir attiecīgais Lagranža
reizinātāju vektors. Stacionārā punkta raksturs ir atkarīgs no
funkcijas pieauguma
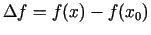 zīmes, kur
zīmes, kur 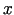 apmierina saites (1.8). Atzīmēsim, ka
apmierina saites (1.8). Atzīmēsim, ka
visiem 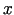 , kuri apmierina nosacījumus (1.8), jo tad
, kuri apmierina nosacījumus (1.8), jo tad
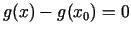 . Tas nozīmē, ka funkcijas pieauguma
. Tas nozīmē, ka funkcijas pieauguma 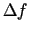 vietā var analizēt
vietā var analizēt 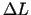 . Iegūstam
. Iegūstam
kur
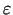 ir augstākas kārtas loceklis attiecībā pret
argumentu pieaugumu. Tā kā
ir augstākas kārtas loceklis attiecībā pret
argumentu pieaugumu. Tā kā
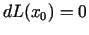 , tad pieauguma
, tad pieauguma 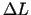 zīme ir atkarīga no kvadrātiskās formas
zīme ir atkarīga no kvadrātiskās formas
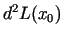 zīmes, kura savukārt ir atkarīga no
zīmes, kura savukārt ir atkarīga no 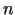 mainīgajiem
mainīgajiem

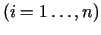 . Diferencējot saites, iegūstam sakarības
. Diferencējot saites, iegūstam sakarības
Pieņemot, ka matricas
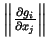 rangs ir
rangs ir  (tas nozīmē, ka vismaz viens šīs matricas
(tas nozīmē, ka vismaz viens šīs matricas
 -tās kārtas minors punktā
-tās kārtas minors punktā 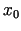 nav vienāds ar nulli, bet
katrs šīs matricas
nav vienāds ar nulli, bet
katrs šīs matricas  -tās kārtas minors punktā
-tās kārtas minors punktā 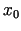 ir
vienāds ar nulli), varam izteikt
ir
vienāds ar nulli), varam izteikt  atkarīgo mainīgo
diferenciāļus ar
atkarīgo mainīgo
diferenciāļus ar  neatkarīgo mainīgo diferenciāļiem. Tad
neatkarīgo mainīgo diferenciāļiem. Tad
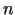 mainīgo kvadrātiskā forma
mainīgo kvadrātiskā forma
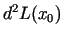 kļūs par
kļūs par  neatkarīgo mainīgo formu
neatkarīgo mainīgo formu 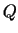 . Šo kvadrātisku formu var pētīt
standarta veidā (skat. 1.1.5. apakšparagrāfu) un spriest
par stacionārā punkta raksturu. Atgādināsim, ka, ja forma
. Šo kvadrātisku formu var pētīt
standarta veidā (skat. 1.1.5. apakšparagrāfu) un spriest
par stacionārā punkta raksturu. Atgādināsim, ka, ja forma 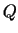 ir
pozitīva, tad punktā
ir
pozitīva, tad punktā 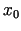 ir minimums (nosacītais!), bet, ja
ir minimums (nosacītais!), bet, ja
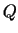 ir negatīva, tad punkts
ir negatīva, tad punkts 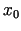 ir nosacītā maksimuma
punkts.
ir nosacītā maksimuma
punkts.
-
1.7. piemērs.
-
a) Lagranža funkcija
Risinot sistēmu
iegūstam stacionāro punktu 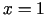 ,
, 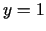 ,
,
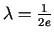 .
.
b) Diferencējot saiti 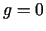 ,
iegūstam sakarību
,
iegūstam sakarību
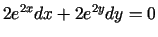 , un punktā
, un punktā 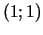 ir
spēkā vienādība
ir
spēkā vienādība
c) Noskaidrojam stacionārā punkta 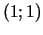 raksturu. Atrodam:
raksturu. Atrodam:
Ja 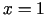 ,
, 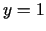 ,
,
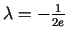 , tad
, tad
Pieņemam 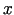 par neatkarīgo mainīgo, bet
par neatkarīgo mainīgo, bet  - par atkarīgo. Tā kā
- par atkarīgo. Tā kā
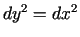 , tad
, tad
un, acīmredzot, kvadrātiskā forma
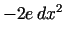 ir negatīva.
ir negatīva.
Secinājums: punktā 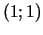 funkcijai
funkcijai 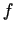 ir nosacītais
maksimums.
ir nosacītais
maksimums.
-
1.8. piemērs.
- Problēma par cilindru ar minimālo virsmas
laukumu pie dotā tilpuma (skat. 1.2.1. apakšparagrāfu)
reducējas uz nosacītā ekstrēma problēmu:
Pieņemsim, ka 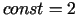 un atradīsim problēmas:
un atradīsim problēmas:
atrisinājumu.
a) Lagranža funkcija
Risinot sistēmu
iegūstam stacionāro punktu: 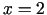 ,
, 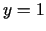 ,
,
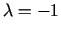 .
.
b) Diferencējot saiti 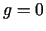 , punktā (2;1) iegūstam sakarību
, punktā (2;1) iegūstam sakarību
c) Noskaidrojam stacionārā punkta raksturu.
Ja 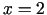 ,
, 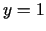 ,
,
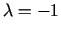 , tad
, tad
Uzskatīsim  par neatkarīgo mainīgo, bet
par neatkarīgo mainīgo, bet 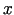 - par atkarīgo. Tā
kā
- par atkarīgo. Tā
kā 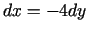 , tad
, tad
un, acīmredzot, kvadrātiskā forma ir pozitīva.
Secinājums: punkts 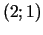 ir nosacītā maksimuma punkts.
ir nosacītā maksimuma punkts.
-
1.9. piemērs.
-
a) Lagranža funkcija
Sistēmai
ir šādi atrisinājumi
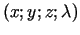 :
:
b) Diferencējot saiti 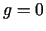 , iegūstam sakarību starp mainīgo
diferenciāļiem
, iegūstam sakarību starp mainīgo
diferenciāļiem
c) Noskaidrojam stacionārā punkta
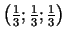 pie
pie
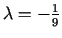 raksturu.
raksturu.
Punktā
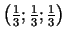 iegūsim:
iegūsim:
Šī kvadrātiskā forma ir negatīva.
Secinājums: punkts
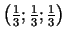 ir funkcijas
ir funkcijas
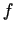 nosacītā minimuma punkts.
nosacītā minimuma punkts.
Pārējos stacionārajos
punktos formas 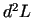 determinants ir vienāds ar nulli. Viegli
saprast, ka funkcija
determinants ir vienāds ar nulli. Viegli
saprast, ka funkcija 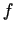 jebkura cita stacionāra punkta
apkārtnē pieņem gan negatīvas, gan pozitīvas vērtības, un līdz
ar to funkcijai
jebkura cita stacionāra punkta
apkārtnē pieņem gan negatīvas, gan pozitīvas vērtības, un līdz
ar to funkcijai 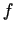 šajos punktos ekstrēma nav.
šajos punktos ekstrēma nav.
Sakarā ar to, ka nosacītā minimuma pietiekamie nosacījumi dažādos
avotos ir izklāstīti dažādi, pievērsīsim uzmanību dažām izplatītām
kļūdām.
1. kļūda. Aplams ir
apgalvojums, ka, lai noskaidrotu Lagranža funkcijas stacionārā
punkta raksturu, pietiek ar Lagranža funkcijas pētīšanu uz brīvo
ekstrēmu pie atrastās parametra 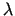 vērtības. Apskatīsim
1.8. piemēru:
vērtības. Apskatīsim
1.8. piemēru:
un izpētīsim Lagranža funkcijas
raksturu stacionārā punktā 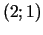 pie
pie
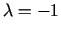 . Atrodam:
. Atrodam:
Kvadrātiskās formas determinants ir vienāds ar 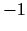 , un no tā seko
aplams apgalvojums, ka ekstrēma dotajā problēmā
nav.
, un no tā seko
aplams apgalvojums, ka ekstrēma dotajā problēmā
nav.
2. kļūda. Aplams ir
apgalvojums, ka, lai noskaidrotu Lagranža funkcijas stacionārā
punkta raksturu, pietiek izpētīt uz ekstrēmu funkciju 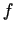 , ņemot
vērā lineārās sakarības starp mainīgo diferenciāļiem, kuras
iegūst, diferencējot saites. Tā 1.7. piemērā
, ņemot
vērā lineārās sakarības starp mainīgo diferenciāļiem, kuras
iegūst, diferencējot saites. Tā 1.7. piemērā
stacionārā punktā 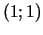 . Kvadrātiskā forma
. Kvadrātiskā forma
ir pozitīva visiem 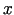 un
un  , bet secinājums, ka funkcijai
, bet secinājums, ka funkcijai 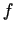 punktā
punktā 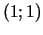 ir nosacītais minimums, ir aplams.
ir nosacītais minimums, ir aplams.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2.10. Uzdevumi
Augstāk: 1.2. Nosacītais ekstrēms
Iepriekšējais: 1.2.8. Uzdevumi
2002-05-04
![]() ir Lagranža funkcijas
ir Lagranža funkcijas
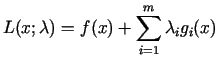
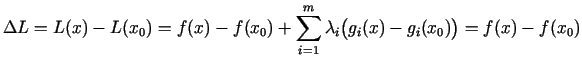
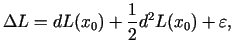
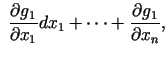
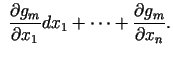
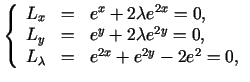
![]() ,
iegūstam sakarību
,
iegūstam sakarību
![]() , un punktā
, un punktā ![]() ir
spēkā vienādība
ir
spēkā vienādība
![]() raksturu. Atrodam:
raksturu. Atrodam:
![]() funkcijai
funkcijai ![]() ir nosacītais
maksimums.
ir nosacītais
maksimums.

![]() , punktā (2;1) iegūstam sakarību
, punktā (2;1) iegūstam sakarību
![]() ir nosacītā maksimuma punkts.
ir nosacītā maksimuma punkts.

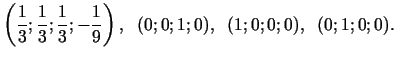
![]() , iegūstam sakarību starp mainīgo
diferenciāļiem
, iegūstam sakarību starp mainīgo
diferenciāļiem
![]() pie
pie
![]() raksturu.
raksturu.
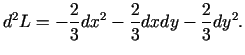
![]() ir funkcijas
ir funkcijas
![]() nosacītā minimuma punkts.
nosacītā minimuma punkts.