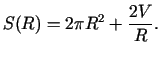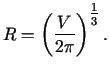Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2.2. Definīcijas
Augstāk: 1.2. Nosacītais ekstrēms
Iepriekšējais: 1.2. Nosacītais ekstrēms
1.2.1. Uzdevumi
1. problēma (joks). Meitenei patīk saņemt dāvanas no
jaunekļa, kas dāvina viņai puķes, maksājot Ls 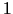 par vienu pušķi,
un šokolādi, kuras cena ir Ls
par vienu pušķi,
un šokolādi, kuras cena ir Ls 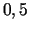 par vienu tāfelīti. Nedēļas
laikā jauneklis var atļauties iztērēt Ls
par vienu tāfelīti. Nedēļas
laikā jauneklis var atļauties iztērēt Ls 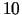 . Kāda dāvanu
kombinācija ir visefektīvākā, ja efektivitāti izsaka funkcija
. Kāda dāvanu
kombinācija ir visefektīvākā, ja efektivitāti izsaka funkcija
kur 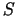 - šokolādes tāfelīšu daudzums,
- šokolādes tāfelīšu daudzums, 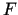 - puķu pušķu
daudzums.
- puķu pušķu
daudzums.
Risinājums. Šokolādes
pirkšanai vajadzīgi Ls 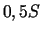 , puķu pirkšanai Ls
, puķu pirkšanai Ls 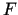 . Kopā
. Kopā
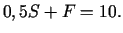 |
(1.2) |
Līdz ar to problēma reducējas uz funkcijas 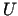 maksimuma atrašanu
pie ierobežojuma (1.2). Risināsim problēmu ar
mainīgo izslēgšanas metodi. No vienādības (1.2)
atrodam
maksimuma atrašanu
pie ierobežojuma (1.2). Risināsim problēmu ar
mainīgo izslēgšanas metodi. No vienādības (1.2)
atrodam
un iegūstam maksimuma problēmu viena argumenta funkcijai
Aprēķinot šīs funkcijas atvasinājumu un pielīdzinot to nullei,
iegūstam vienādojumu, no kura izriet, ka 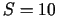 ,
,
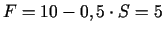 . Tātad jauneklis nedēļas laikā var nopirkt
. Tātad jauneklis nedēļas laikā var nopirkt 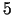 puķu pušķus un
puķu pušķus un 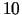 šokolādes plāksnītes.
šokolādes plāksnītes.
Aplūkosim analoģisku problēmu ar nopietnāku
saturu.
2. problēma. Firma iegulda
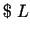 personāla apmaksai un
personāla apmaksai un 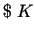 tehnisko līdzekļu
pirkšanai. Saražotās produkcijas apjoms ir atkarīgs no
ieguldītajiem līdzekļiem:
tehnisko līdzekļu
pirkšanai. Saražotās produkcijas apjoms ir atkarīgs no
ieguldītajiem līdzekļiem:
Kopējais līdzekļu apjoms ir
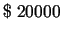 . Cik daudz līdzekļu ir
jāizlieto personāla apmaksai (un cik tehnisko līdzekļu iegādei),
lai maksimizētu ražošanas apjomu?
. Cik daudz līdzekļu ir
jāizlieto personāla apmaksai (un cik tehnisko līdzekļu iegādei),
lai maksimizētu ražošanas apjomu?
Risinājums. Lietosim mainīgo izslēgšanas metodi. Tā kā
tad
un problēma reducējas uz funkcijas
maksimuma atrašanu. Aprēķinot atvasinājumu
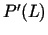 un
pielīdzinot to nullei, iegūstam vienādojumu
un
pielīdzinot to nullei, iegūstam vienādojumu
no kura izriet, ka 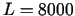 ,
, 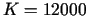 . Tātad, lai maksimizētu
ražošanu, personāla apmaksai ir jāpiešķir
. Tātad, lai maksimizētu
ražošanu, personāla apmaksai ir jāpiešķir
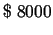 , bet
tehnisko līdzekļu iegādei -
, bet
tehnisko līdzekļu iegādei -
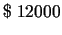 .
.
3. problēma. Cilindriskas formas degvielas krātuves
tilpums ir vienāds ar 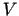 . Kādiem
. Kādiem 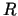 (- cilindra rādiuss) un
(- cilindra rādiuss) un 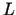 (- cilindra augstums) virsmas laukums
(- cilindra augstums) virsmas laukums 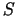 (un līdz ar to arī
materiāla patēriņš) būs minimāls (skat.
1.3. zīm.)?
(un līdz ar to arī
materiāla patēriņš) būs minimāls (skat.
1.3. zīm.)?
Risinājums.
Virsmas laukums
Tātad problēma reducējas uz funkcijas
minimuma atrašanu, ja
Ievietojot
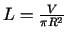 lieluma
lieluma 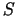 aprēķināšanas
formulā, iegūstam brīvā ekstrēma problēmu (par brīvā
ekstrēma problēmu sauc ekstrēmu problēmu bez
ierobežojumiem) viena argumenta funkcijai
aprēķināšanas
formulā, iegūstam brīvā ekstrēma problēmu (par brīvā
ekstrēma problēmu sauc ekstrēmu problēmu bez
ierobežojumiem) viena argumenta funkcijai
Aprēķinot šīs funkcijas atvasinājumu un pielīdzinot to nullei,
iegūstam vienādojumu
no kura atrodam, ka



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2.2. Definīcijas
Augstāk: 1.2. Nosacītais ekstrēms
Iepriekšējais: 1.2. Nosacītais ekstrēms
2002-05-04
![]() par vienu pušķi,
un šokolādi, kuras cena ir Ls
par vienu pušķi,
un šokolādi, kuras cena ir Ls ![]() par vienu tāfelīti. Nedēļas
laikā jauneklis var atļauties iztērēt Ls
par vienu tāfelīti. Nedēļas
laikā jauneklis var atļauties iztērēt Ls ![]() . Kāda dāvanu
kombinācija ir visefektīvākā, ja efektivitāti izsaka funkcija
. Kāda dāvanu
kombinācija ir visefektīvākā, ja efektivitāti izsaka funkcija
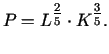
![]() . Kādiem
. Kādiem ![]() (- cilindra rādiuss) un
(- cilindra rādiuss) un ![]() (- cilindra augstums) virsmas laukums
(- cilindra augstums) virsmas laukums ![]() (un līdz ar to arī
materiāla patēriņš) būs minimāls (skat.
1.3. zīm.)?
(un līdz ar to arī
materiāla patēriņš) būs minimāls (skat.
1.3. zīm.)?