


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2. SKAITLISKĀS METODES
Augstāk: 1.2. Nosacītais ekstrēms
Iepriekšējais: 1.2.9. Nosacītā ekstrēma pietiekamie nosacījumi
- 7.
Atrast ekstrēma punktus un noteikt to raksturu, izmantojot mainīgo
izslēgšanas metodi, šādās problēmās:
- 7a.
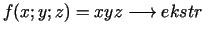 ,
,
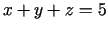 ,
,
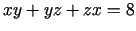 ;
;
- 7b.
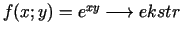 ,
, 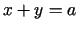 ;
;
- 7c.
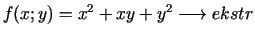 ,
, 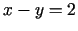 ;
;
- 7d.
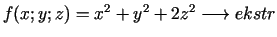 ,
, 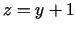 ;
;
- 7e.
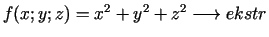 ,
,
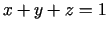 ,
,
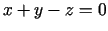 .
.
- 8.
Atrast ekstrēma punktus un noteikt to raksturu, izmantojot
Lagranža reizinātāju metodi, šādās problēmās:
- 8a.
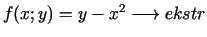 ,
,
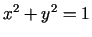 ;
;
- 8b.
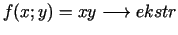 ,
,
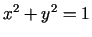 ;
;
- 8c.
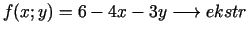 ,
,
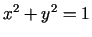 ;
;
- 8d.
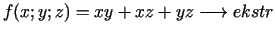 ,
, 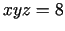 .
.
- 9.
Starp visiem
taisnstūra paralēlskaldņiem (ar šķautnēm  ,
, 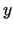 ,
,  ) ar doto
šķautņu summu
) ar doto
šķautņu summu
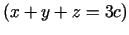 atrast to, kuram tilpums ir
vislielākais.
atrast to, kuram tilpums ir
vislielākais.
2002-05-04